Plantilla:Dominio e imagen de una función
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:58 20 ene 2009 Coordinador (Discusión | contribuciones) (→Dominio e imagen de una función) ← Ir a diferencia anterior |
Revisión de 17:58 20 ene 2009 Coordinador (Discusión | contribuciones) (→Dominio e imagen de una función) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| ==Dominio e imagen de una función== | ==Dominio e imagen de una función== | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | *Al conjunto de los valores que puede tomar la variable independiente <math>x\;</math>, se le llama '''dominio de definición''' de la función. lo representaremos por <math>D, \ D_f\;</math> ó <math>Dom_f\;</math> | + | *Al conjunto de los valores que puede tomar la variable independiente <math>x\;</math>, se le llama '''dominio de definición''' de la función. Lo representaremos por <math>D, \ D_f\;</math> ó <math>Dom_f\;</math> |
| *La '''imagen''' o '''recorrido''' de una función es el conjunto de valores que toma la variable dependiente <math>y\;</math>. Lo representaremos por <math>Im_f\;</math>. | *La '''imagen''' o '''recorrido''' de una función es el conjunto de valores que toma la variable dependiente <math>y\;</math>. Lo representaremos por <math>Im_f\;</math>. | ||
| }} | }} | ||
Revisión de 17:58 20 ene 2009
Dominio e imagen de una función
- Al conjunto de los valores que puede tomar la variable independiente
, se le llama dominio de definición de la función. Lo representaremos por 
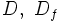ó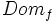 
- La imagen o recorrido de una función es el conjunto de valores que toma la variable dependiente
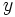. Lo representaremos por 
.
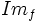Razones para restringir el dominio de una función
- Imposibilidad de realizar alguna operación con ciertos valores de (Por ejemplo: denominadores que se anulan, radicandos que toman valores negativos,...)
- Contexto en el que se estudia la función (Por ejemplo, una función que relaciona lado y área de una figura plana, no puede tomar valores negativos
- Por voluntad de quien propone la función.
Ejemplo: Dominio de una función
- Halla el dominio de las funciones:
- a)
![y=x-3 \ , \quad x \in [-1,1]\;\!](/wikipedia/images/math/b/2/f/b2f9332046e953e44d840dc3a97e95ea.png)
- a)
- b)
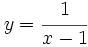
- b)
- c)
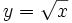
- c)
- d)
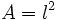(Área de un cuadrado de lado 
)
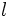- d)
Solución:
- a) Su dominio es
![[-1,1]\;\!](/wikipedia/images/math/d/e/f/defe3e8e42c39a844e648621afe1619e.png)
, por voluntad del que ha definido la función, ya que, en principio, cualquier valor de da un valor de 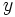válido.
- b) Su dominio es
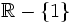, porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
- c) Su dominio es
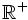, porque el radicando no puede ser negativo para poder hallar la raíz.
- d) Su dominio es
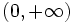, porque el lado de un cuadrado sólo puede tomar valores positivos
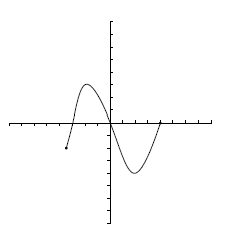
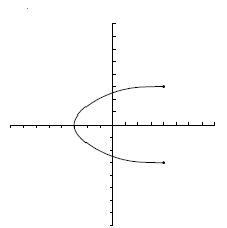
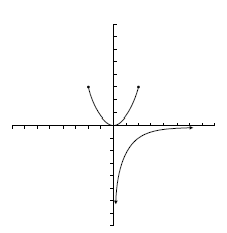
 Ejercicios: Dominio e imagen 1. Indica cuál de las gráficas siguientes representan una función. En caso de ser función, indica su dominio y su imagen. Solución: a) Es función. ![D=[-3.5, 4]\;\!](/wikipedia/images/math/6/f/4/6f4030ef099e99944025cbb34e75c6ae.png) . ![Im=[-4, 3]\;\!](/wikipedia/images/math/4/9/c/49cf9064f7a20c06eb8cb9c71af85beb.png) .
b) No es función. |
