Función inversa o recíproca (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:48 24 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:54 24 ene 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 7: | Línea 7: | ||
| {{p}} | {{p}} | ||
| ==Función inversa o recíproca== | ==Función inversa o recíproca== | ||
| - | {{Tabla75|celda2= | ||
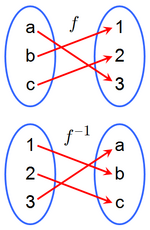
| - | <center>[[Imagen:Inverse Function.png|thumb|150px|Una función ƒ y su inversa o recíproca ƒ<sup> –1</sup>. Como ƒ aplica ''a'' en 3, la inversa ƒ<sup> –1</sup> lleva 3 de vuelta en ''a''.]]</center> | ||
| - | |celda1= | ||
| Si <math>f\;</math> es una función que lleva elementos de <math>X\;</math> en elementos de <math>Y\;</math>, en ciertas condiciones será posible definir la aplicación <math>f^{-1}\;</math> que realice el camino de vuelta de <math>Y\;</math> a <math>X\;</math>. En ese caso diremos que <math>f^{-1}\;</math> es la función '''inversa''' o '''recíproca''' de <math>f\;</math>. Formalmente: | Si <math>f\;</math> es una función que lleva elementos de <math>X\;</math> en elementos de <math>Y\;</math>, en ciertas condiciones será posible definir la aplicación <math>f^{-1}\;</math> que realice el camino de vuelta de <math>Y\;</math> a <math>X\;</math>. En ese caso diremos que <math>f^{-1}\;</math> es la función '''inversa''' o '''recíproca''' de <math>f\;</math>. Formalmente: | ||
| {{p}} | {{p}} | ||
| + | {{Tabla75|celda2=<center>[[Imagen:Inverse Function.png|thumb|150px|Una función ƒ y su inversa o recíproca ƒ<sup> –1</sup>. Como ƒ aplica ''a'' en 3, la inversa ƒ<sup> –1</sup> lleva 3 de vuelta en ''a''.]]</center> | ||
| + | |celda1= | ||
| {{Caja_Amarilla | {{Caja_Amarilla | ||
| |texto= | |texto= | ||
| Línea 23: | Línea 22: | ||
| |enunciado= | |enunciado= | ||
| {{p}} | {{p}} | ||
| - | ::*Las gráficas de <math>f\;</math> y <math>f^{-1}\;</math> son simétricas respecto de la recta y=x. | + | ::*Las gráficas de <math>f\;</math> y <math>f^{-1}\;</math> son simétricas respecto de la recta <math>y=x\;</math>. |
| ::*La función <math>f^{-1}\;</math>, al igual que <math>f\;</math>, es una función [[Función biyectiva|biyectiva]], que queda determinada de modo único por <math>f\;</math> y que cumple: | ::*La función <math>f^{-1}\;</math>, al igual que <math>f\;</math>, es una función [[Función biyectiva|biyectiva]], que queda determinada de modo único por <math>f\;</math> y que cumple: | ||
| :::a) <math>f^{-1} \circ f = I_X</math> | :::a) <math>f^{-1} \circ f = I_X</math> | ||
Revisión de 16:54 24 ene 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Función inversa o recíproca
Si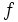 
es una función que lleva elementos de 
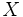en elementos de 
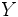, en ciertas condiciones será posible definir la aplicación 
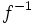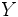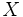que realice el camino de vuelta de a . En ese caso diremos que 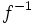es la función inversa o recíproca de 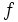. Formalmente:
Sea 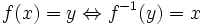  Propiedades
Demostración: |  |
.
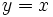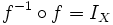
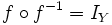
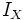e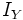 
son las funciones identidad en 
