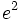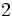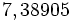Funciones exponenciales (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 14:31 25 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 14:33 25 ene 2009 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 52: | Línea 52: | ||
| }} | }} | ||
| }} | }} | ||
| - | {{p}} | ||
| {{Tabla75 | {{Tabla75 | ||
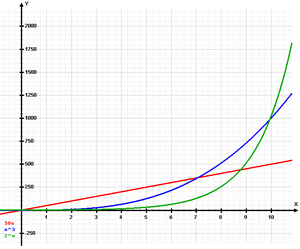
| |celda2=[[Image:Exponential.png|thumb|right|300px|Comparación entre el crecimiento lineal (rojo), crecimiento potencial (azul) y crecimiento exponencial (verde)]] | |celda2=[[Image:Exponential.png|thumb|right|300px|Comparación entre el crecimiento lineal (rojo), crecimiento potencial (azul) y crecimiento exponencial (verde)]] | ||
Revisión de 14:33 25 ene 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Función exponencial de base a
Sea 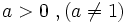 un número real. Se define la función exponencial de base
un número real. Se define la función exponencial de base  como:
como:
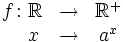
La función exponencial de base e (número e) es de especial importancia en matemáticas y se denomina simplementre función exponencial, sin hacer mención a la base.
|
Actividad Interactiva: Función exponencial
Actividad 1. Representación gráfica de distintas funciones exponenciales.
Actividad: En esta escena tienes las gráfica de las funciones: a)
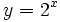 (en verde); b) (en verde); b) 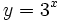 (en amarillo); c) (en amarillo); c) 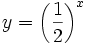 (en rojo); d) (en rojo); d) 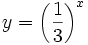 (en turquesa) (en turquesa)Comprueba en la escena anterior las siguientes propiedades:
|
Calculadora
Exponencial de base 10
|
Calculadora: Exponencial de base 10 |
Exponencial de base e
|
Calculadora: Exponencial de base e |
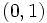 y
y 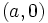 , donde
, donde 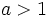 , son crecientes y si
, son crecientes y si 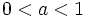 decrecientes.
decrecientes.
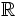 .
.
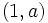 .
.
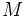 que crece con el tiempo
que crece con el tiempo 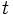 de acuerdo con la ecuación:
de acuerdo con la ecuación:
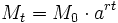
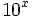 usaremos la tecla
usaremos la tecla 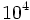
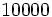
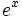 usaremos la tecla
usaremos la tecla