Números complejos: Operaciones en forma polar (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 12:40 11 mar 2009 Coordinador (Discusión | contribuciones) (→Fórmula de Moivre) ← Ir a diferencia anterior |
Revisión de 12:43 11 mar 2009 Coordinador (Discusión | contribuciones) (→Fórmula de Moivre) Ir a siguiente diferencia → |
||
| Línea 61: | Línea 61: | ||
| {{p}} | {{p}} | ||
| ===Fórmula de Moivre=== | ===Fórmula de Moivre=== | ||
| - | {{Teorema|titulo=Fórmula de Moivre|enunciado=La fórmula | + | {{Teorema|titulo=Fórmula de Moivre|enunciado= |
| - | {{p}} | + | |
| {{Caja|contenido=<math>(cos \, \alpha + i \, sen \, \alpha)^n=cos \, (n \, \alpha) + i \, sen \, (n \, \alpha)</math>}} | {{Caja|contenido=<math>(cos \, \alpha + i \, sen \, \alpha)^n=cos \, (n \, \alpha) + i \, sen \, (n \, \alpha)</math>}} | ||
| - | + | {{p}} | |
| - | debe su nombre a [[Moivre]]. | + | Esta fórmula debe su nombre al matemático francés [[Abraham de Moivre|Moivre]] (1667 - 1754). |
| |demo= | |demo= | ||
| Basta aplicar la fórmula de la potencia de un complejo en forma polar y tener en cuenta la forma trigonométrica de un número complejo. | Basta aplicar la fórmula de la potencia de un complejo en forma polar y tener en cuenta la forma trigonométrica de un número complejo. | ||
Revisión de 12:43 11 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Multiplicación de números complejos en forma polar
El producto de dos numeros complejos en forma polar es otro complejo en forma polar cuyo módulo es el producto de los módulos y el argumento la suma de los argumentos de los respectivos complejos.
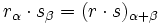
|
Actividad interactiva: Multiplicación de complejos en forma polar
|
Potencias de números complejos en forma polar
La potencia n-ésima de un compejo es el resultado de multiplicar dicho complejo por sí mismo n veces, por tanto, aplicando la fórmula del producto:
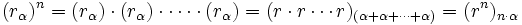
|
Actividad interactiva: Potencias de complejos en forma polar
|
Fórmula de Moivre
Fórmula de Moivre
Demostración:
Basta aplicar la fórmula de la potencia de un complejo en forma polar y tener en cuenta la forma trigonométrica de un número complejo.
División de números complejos en forma polar
|
Actividad interactiva: División de complejos en forma polar
|
Radicación de números complejos en forma polar
|
Actividad interactiva: Raíces de complejos en forma polar
|
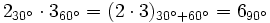
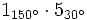
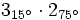
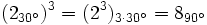
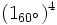 b)
b) 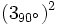 c)
c)  d)
d) 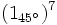
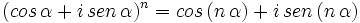
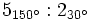
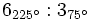
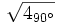 b)
b) ![\sqrt[3]{8_{120^\circ}}](/wikipedia/images/math/0/2/9/02928c662b770c320d65ec6f6ebb988d.png) c)
c) ![\sqrt[5]{5_{270^\circ}}](/wikipedia/images/math/a/a/9/aa96d66344414293e64e280028494f05.png) d)
d) ![\sqrt[4]{6_{120^\circ}}](/wikipedia/images/math/5/b/2/5b29523f5dc1a2d4bbc07a377e06bae8.png)

