Puntos y vectores el plano (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:26 16 mar 2009 Coordinador (Discusión | contribuciones) (→Sistema de referencia en el plano) ← Ir a diferencia anterior |
Revisión de 18:51 16 mar 2009 Coordinador (Discusión | contribuciones) (→Sistema de referencia en el plano) Ir a siguiente diferencia → |
||
| Línea 7: | Línea 7: | ||
| {{p}} | {{p}} | ||
| ==Sistema de referencia en el plano== | ==Sistema de referencia en el plano== | ||
| - | {{Caja_Amarilla|texto=Un '''sistema de referencia''' del plano consiste en una terna <math>\mathcal{R}={O,(\overrightarrow{x},\overrightarrow{y})}</math> | + | {{Caja_Amarilla|texto=Un '''sistema de referencia''' del plano consiste en una terna {{sube|porcentaje=+20%|contenido=<math>\mathfrak{R}=\big\{O,(\overrightarrow{x},\overrightarrow{y})\big\}</math>}}, donde {{sube|porcentaje=+20%|contenido=<math>O\,</math>}} es un punto fijo, llamado '''origen''', y {{sube|porcentaje=+20%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}} una base de vectores del plano. |
| }} | }} | ||
| + | {{p}} | ||
| + | {{Caja_Amarilla|texto=En un sistema de referencia {{sube|porcentaje=+20%|contenido=<math>\mathfrak{R}=\big\{O,(\overrightarrow{x},\overrightarrow{y})\big\}</math>}}, cada punto <math>P\,</math> del plano tiene asociado un vector fijo {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{OP}</math>}}, llamado '''vector de posición''' del punto <math>P\,</math>. | ||
| + | |||
| + | Si el vector {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{OP}</math>}} tiene coordenadas <math>(a,b)\,</math> respecto de la base {{sube|porcentaje=+20%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}}, el punto <math>P\,</math> tendrá coordenadas <math>(a,b)\,</math> respecto del sistema de referencia {{sube|porcentaje=+20%|contenido=<math>\mathfrak{R}</math>}}. | ||
| + | }} | ||
| + | {{p}} | ||
| ==Vector de posición== | ==Vector de posición== | ||
Revisión de 18:51 16 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Sistema de referencia en el plano
Un sistema de referencia del plano consiste en una terna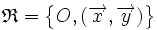 
, donde 
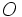es un punto fijo, llamado origen, y 
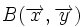una base de vectores del plano.
En un sistema de referencia 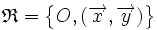, cada punto 
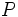del plano tiene asociado un vector fijo 
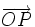, llamado vector de posición del punto .
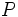Si el vector 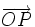tiene coordenadas 
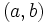respecto de la base 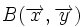, el punto 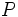tendrá coordenadas 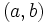respecto del sistema de referencia 
.
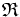