Distancias en el plano (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 21:57 23 mar 2009 Coordinador (Discusión | contribuciones) (→Distancia de un punto a una recta) ← Ir a diferencia anterior |
Revisión de 22:28 23 mar 2009 Coordinador (Discusión | contribuciones) (→Distancia de un punto a una recta) Ir a siguiente diferencia → |
||
| Línea 40: | Línea 40: | ||
| {{Caja|contenido=<math>d(P,r)=\cfrac{|Aa+Bb+C|}{\sqrt{A^2+B^2}}</math>}} | {{Caja|contenido=<math>d(P,r)=\cfrac{|Aa+Bb+C|}{\sqrt{A^2+B^2}}</math>}} | ||
| - | |demo= | + | |demo=[[Imagen:distpuntorecta.png|right]] |
| + | Sea <math>R(x_0,y_0)\,</math> un punto de la recta. | ||
| + | |||
| + | Dados dos vectores {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}</math>}} y {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}}, sabemos que <math>proy_{\overrightarrow{u}}\overrightarrow{v}=\cfrac{\overrightarrow{u} \cdot \overrightarrow{v}}{|\overrightarrow{u}|}</math> (I) | ||
| + | |||
| + | Llamando {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{u}=\overrightarrow{n}=(A,B)</math>}}, {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}=\overrightarrow{RP}=(a-x_0,b-y_0)</math>}} | ||
| + | |||
| + | :<math>d(P,R)=proy_{\overrightarrow{u}}\overrightarrow{v}=\cfrac{\overrightarrow{n} \cdot \overrightarrow{RP}}{|\overrightarrow{n}|}=\cfrac{|(A,B) \cdot (a-x_0,b-y_0)}{|(A,B)|}=</math> | ||
| + | :<math>=\cfrac{|A(a-x_0)+B(b-y_0)}{\sqrt{A^2+B^2}}=\cfrac{|Aa+Bb-(Ax_0+By_0)}{\sqrt{A^2+B^2}}=\cfrac{|Aa+Bb+C)}{\sqrt{A^2+B^2}}</math> | ||
| + | |||
| + | ya que <math>Ax_0+By_0=-C\,</math>, por ser <math>R(x_0,y_0)\,</math> un punto de la recta. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 22:28 23 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Distancia ente dos puntos
La distancia entre dos puntos 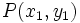 y
y 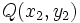 es igual al módulo del vector
es igual al módulo del vector 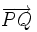 :
:
|
|
|
Actividad Interactiva: Distancia entre dos puntos
Actividad 1: En esta escena vamos a hallar la distancia entre los puntos
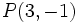 y y 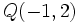 . .Actividad: 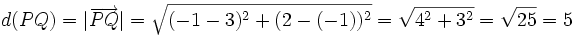
Ejercicio: Calcula la distancia entre los puntos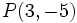 y y 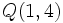 y comprueba el resultado en la escena anterior. y comprueba el resultado en la escena anterior. |
Distancia de un punto a una recta
Proposición
La distancia del punto 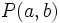 a la recta
a la recta 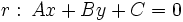 es:
es:
|
|
|
Actividad Interactiva: Distancia de un punto a una recta
Actividad 1: En esta escena vamos a hallar la distancia del punto
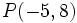 a la recta a la recta 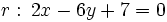 . .Actividad: 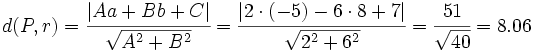
Ejercicio: Calcula la distancia del punto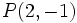 a la recta a la recta 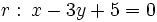 y comprueba el resultado en la escena anterior. y comprueba el resultado en la escena anterior. |
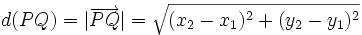
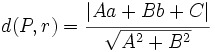
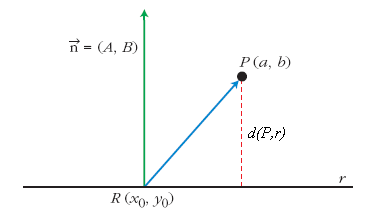
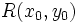 un punto de la recta.
un punto de la recta.
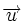
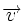
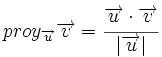 (I)
(I)
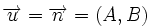
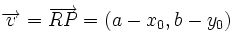
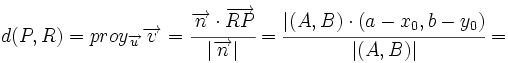
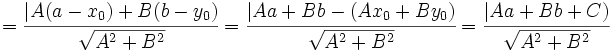
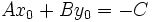 , por ser
, por ser 
