Plantilla:Utilidad de la derivada (1ºBach)
De Wikipedia
| Revisión de 07:11 13 abr 2009 Coordinador (Discusión | contribuciones) (→Problemas de optimización) ← Ir a diferencia anterior |
Revisión de 07:15 13 abr 2009 Coordinador (Discusión | contribuciones) (→Problemas de optimización) Ir a siguiente diferencia → |
||
| Línea 228: | Línea 228: | ||
| </iframe></center> | </iframe></center> | ||
| <center>[http://maralboran.org/web_ma/geogebra/figuras/optimiza_3b.html '''Click''' aquí si no se ve bien la escena]</center> | <center>[http://maralboran.org/web_ma/geogebra/figuras/optimiza_3b.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | |||
| + | }} | ||
| + | {{ai_cuerpo | ||
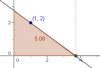
| + | |enunciado='''Problema 4:''' [[Imagen:optimizacion4.gif|left]]:a) De todas las rectas que pasan por el punto (1,2), encuentra la que determina con los ejes de coordenadas, y en el primer cuadrante, un triángulo de área mínima. | ||
| + | :b) Igual que el aprtadoa a), pero para un punto cualquiera del primer cuadrante, en lugar de (1,2). | ||
| + | {{p}} | ||
| + | |||
| + | |actividad= | ||
| + | Observa la figura. Mueve el punto verde y observa los cambios: | ||
| + | *¿Qué representa el punto rojo de la gráfica? | ||
| + | *¿Qué relación hay entre sus coordenadas y el problema? | ||
| + | |||
| + | Haz clic derecho sobre el punto citado y activa "el trazo". Vuelve a mover el punto verde: | ||
| + | *¿Qué punto de la gráfica resultante corresponderá a la solución del problema? | ||
| + | *Compruébalo mediante el deslizador de la parte inferior de la pantalla. | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.org/web_ma/geogebra/figuras/optimiza_4.html | ||
| + | width=780 | ||
| + | height=460 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | <center>[http://maralboran.org/web_ma/geogebra/figuras/optimiza_4.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | |||
| }} | }} | ||
Revisión de 07:15 13 abr 2009
Tabla de contenidos |
Estudio del crecimiento
Estudio de los puntos extremos
Extremos relativos
Ejemplos: Determinación de los extremos relativos
Cálculo de máximos y mínimos relativos
- 10 ejemplos
- 8 ejemplos
- 4 ejemplos
- 3 ejemplos
- 5 ejemplos
- 3 ejemplos
Extremos absolutos
Ejemplos: Determinación de máximos y mínimos absolutos
Cálculo de máximos y mínimos absolutos
- 2 ejemplo2
Problemas de optimización
Problemas de optimización
Ejemplos: Optimización
Problemas de optimización
- 4 ejemplo2
- 3 ejemplo2
- 3 ejemplo2
- 2 ejemplo2
|
Actividad interactiva: Problemas de optimización
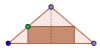
Problema 1: Hallar las dimensiones del rectángulo de área máxima que puede inscribirse en un triángulo isósceles cuya base (lado desigual) mide 8 cm y la altura correspondiente 3 cm (suponiendo que un lado del rectángulo está sobre la base del triángulo).
Actividad: Observa la figura. Mueve el punto verde y observa los cambios:
Haz clic derecho sobre el punto citado y activa "el trazo". Vuelve a mover el punto verde:
Repite el proceso para un triángulo de 6 cm de base y 5 cm de altura. Experimenta e intenta encontrar alguna regularidad en las soluciones.
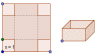
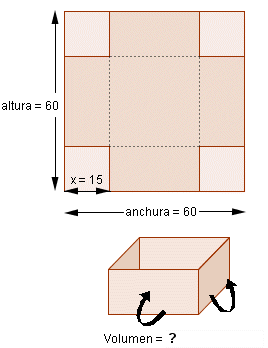
Problema 2: Queremos construir una caja (sin tapa), a partir de una cartulina cuadrada de 6 dm de lado, a la que se recortarán las esquinas. Hallar las dimensiones de las citadas esquinas para que el volumen de la caja sea máximo.
Actividad: Observa la figura. Mueve el punto verde y observa los cambios:
Haz clic derecho sobre el punto citado y activa "el trazo". Vuelve a mover el punto verde:
Repite el proceso para una cartulina cuadrada de 4 cm de lado. ¿Y si la cartulina es un rectángulo de dimensiones 8x5 cm?
GUIÓN DE TRABAJO:
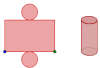
Problema 3: Queremos construir una lata de un tercio de litro de capacidad.
Actividad: Apartado a): Observa la figura. Mueve el punto verde y observa los cambios:
Haz clic derecho sobre el punto citado y activa "el trazo". Vuelve a mover el punto verde:
Apartado b):
Problema 4: :a) De todas las rectas que pasan por el punto (1,2), encuentra la que determina con los ejes de coordenadas, y en el primer cuadrante, un triángulo de área mínima.
Actividad: Observa la figura. Mueve el punto verde y observa los cambios:
Haz clic derecho sobre el punto citado y activa "el trazo". Vuelve a mover el punto verde:
|
Para ampliar
Calculo de la velocidad instantanea de un móvil.
Video tutorial de matematicasbachiller.com
Ejemplos: La sustancia de la derivada
Aproximaciones de números
1 ejemplo
3 ejemplos
Calculo de la variación porcentual.
Video tutorial de matematicasbachiller.com