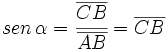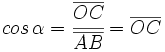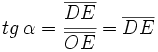Razones trigonométricas de ángulos cualesquiera (1ºBach)
De Wikipedia
| Revisión de 20:45 20 feb 2009 Coordinador (Discusión | contribuciones) (→Relaciones fundamentales de la trigonometría (ángulos de cualquier cuadrante)) ← Ir a diferencia anterior |
Revisión de 12:06 28 sep 2014 Coordinador (Discusión | contribuciones) (→Razones trigonométricas de algunos ángulos importantes) Ir a siguiente diferencia → |
||
| Línea 65: | Línea 65: | ||
| }} | }} | ||
| - | ==Razones trigonométricas de algunos ángulos importantes== | + | |
| - | A continuación las razones trigonométricas de algunos ángulos que es conveniente recordar: | + | |
| - | {{p}} | + | |
| - | {| {{tablabonita_blanca}} | + | |
| - | |-style="background:#e1ecf7;" align="center" | + | |
| - | ! '''Radianes''' | + | |
| - | ! '''Grados''' | + | |
| - | ! sen | + | |
| - | ! cos | + | |
| - | ! tg | + | |
| - | ! cosec | + | |
| - | ! sec | + | |
| - | ! cot | + | |
| - | |----- | + | |
| - | | align="center" | <math> 0 \; </math> | + | |
| - | | align="center" | <math>0^o \,</math> | + | |
| - | | align="center" | <math>0 \;</math> | + | |
| - | | align="center" | <math>1 \;</math> | + | |
| - | | align="center" | <math>0 \;</math> | + | |
| - | | align="center" | <math>\not{\exists} \,\!</math> | + | |
| - | | align="center" | <math>1 \;</math> | + | |
| - | | align="center" | <math>\not{\exists} \,\!</math> | + | |
| - | |----- | + | |
| - | | align="center" | <math> \frac{\pi}{6} </math> | + | |
| - | | align="center" | <math>30^o \,</math> | + | |
| - | | align="center" | <math>\frac{1}{2}</math> | + | |
| - | | align="center" | <math>\frac{\sqrt{3}}{2}</math> | + | |
| - | | align="center" | <math>\frac{\sqrt{3}}{3}</math> | + | |
| - | | align="center" | <math>2 \,</math> | + | |
| - | | align="center" | <math>\frac{2\sqrt{3}}{3}</math> | + | |
| - | | align="center" | <math>\sqrt{3}</math> | + | |
| - | |----- | + | |
| - | | align="center" | <math> \frac{\pi}{4} </math> | + | |
| - | | align="center" | <math>45^o \,</math> | + | |
| - | | align="center" | <math>\frac{\sqrt{2}}{2}</math> | + | |
| - | | align="center" | <math>\frac{\sqrt{2}}{2}</math> | + | |
| - | | align="center" | <math>1 \,</math> | + | |
| - | | align="center" | <math>\sqrt{2}</math> | + | |
| - | | align="center" | <math>\sqrt{2}</math> | + | |
| - | | align="center" | <math>1 \,</math> | + | |
| - | |----- | + | |
| - | | align="center" | <math> \frac{\pi}{3} </math> | + | |
| - | | align="center" | <math>60^o \,</math> | + | |
| - | | <math>\frac{\sqrt{3}}{2}</math> | + | |
| - | | align="center" | <math>\frac{1}{2}</math> | + | |
| - | | align="center" | <math>\sqrt{3}</math> | + | |
| - | | align="center" | <math>\frac{2\sqrt{3}}{3}</math> | + | |
| - | | align="center" | <math>2 \,</math> | + | |
| - | | align="center" | <math>\frac{\sqrt{3}}{3}</math> | + | |
| - | |----- | + | |
| - | | align="center" | <math> \frac{\pi}{2}</math> | + | |
| - | | align="center" | <math>90^o \,</math> | + | |
| - | | align="center" | <math>1 \;</math> | + | |
| - | | align="center" | <math>0 \;</math> | + | |
| - | | align="center" | <math>\not{\exists} \,\!</math> | + | |
| - | | align="center" | <math>1 \,</math> | + | |
| - | | align="center" | <math>\not{\exists} \,\!</math> | + | |
| - | | align="center" | <math>0 \,</math> | + | |
| - | |} | + | |
| - | {{p}} | + | |
| ==Video== | ==Video== | ||
Revisión de 12:06 28 sep 2014
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Circunferencia goniométrica
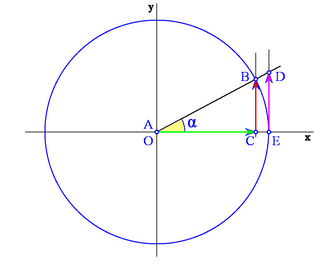
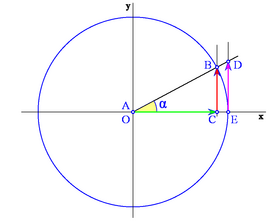
Vamos a establecer un sistema de referencia para el estudio de los ángulos de cualquier cuadrante.
Consideremos una circunferencia de radio 1 centrada en un sistema de referencia cartesiano, es decir, con su centro en el origen de coordenadas O. Sobre ella situaremos nuestro triángulo rectángulo ABC, haciendo coincidir su vértice A con O, el cateto contiguo al ángulo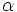 
lo situaremos en el eje X positivo y la hipotenusa coincidiendo con el radio, tal y como se muestra en la figura. A esta circunferencia la llamaremos circunferencia goniométrica.
Teniendo en cuenta que 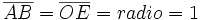 , las razones trigonométricas del águlo se expresan de la siguiente manera:
|  |
Razones trigonométricas de un ángulo cualquiera
Obsérvese como las coordenadas del punto B son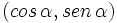 
. Y por extensión, podemos dar la siguiente definición del seno y del coseno de un ángulo de cualquier cuadrante:
Dado un ángulo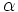 
, se define el coseno y el seno de dicho ángulo, como las coordenadas del punto de corte del segundo lado del ángulo con la circunferencia goniométrica:
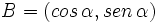
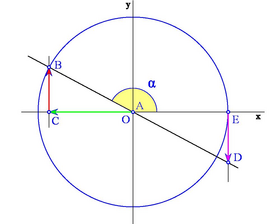
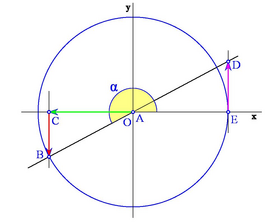
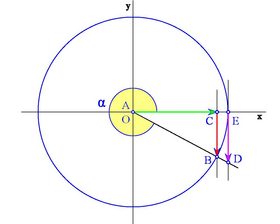
Signo de las razones trigonométricas
Según en qué cuadrante estemos, el segmento OC que determina al coseno, puede estar situado a la derecha o a la izquierda del origen O. Así, asignaremos signo positivo al coseno si está a la derecha de O y negativo si está a la izquierda.
Analogamente, el segmento CB que determina al seno, puede estar situado por encima o por debajo del eje X . Asignaremos signo positivo al seno si está por encima y negativo si está por debajo.
Los siguientes gráficos muestran los distintos casos según en qué cuadrante se encuentre el ángulo:
Cuadrante I
( seno + / cos + ) | Cuadrante II
( seno + / cos - )  |
Cuadrante III
( seno - / cos - )  | Cuadrante IV
( seno - / cos + )  |
Relaciones fundamentales de la trigonometría (ángulos de cualquier cuadrante)
Las relaciones fundamentales de la trigonometría, ya estudiadas anteriormente, siguen siendo válidas con las definiciones dadas para ángulos de cualquier cuadrante.
 Actividad interactiva: Relaciones fundamentales de la trigonometría
Actividad 1: Practica con las relaciones fundamentales de la trigonometría y ponte a prueba con una autoevaluación. En estas actividades tendrás que tener en cuenta en qué cuadrante está el ángulo para determinar el signo de la razón trigonométrica.
Actividad:
|
Video
Círculo Goniométrico (12'55") Sinopsis: - Razones trigonométricas de un ángulo. Fórmula fundamental.
- Circúlo goniométrico.
- Interpretación geométrica de las razones trigonométricas.
- Medida en grados y radianes.
- Tablas de las razones trigonométricas de los ángulos principales.
- Signo de las razones trigonométricas segun el cuadrante del ángulo.
