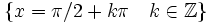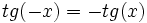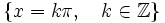Funciones trigonométricas o circulares (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 16:50 30 sep 2014 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:33 15 oct 2014 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 88: | Línea 88: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{wolfram | ||
| + | |titulo=Actividad: ''Funciones trigonométricas'' | ||
| + | |cuerpo= | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | |||
| + | :Representación de las funciones: sen(x), cos(x), tg(x), cosec(x), sec(x), cotg(x) | ||
| + | {{p}} | ||
| + | |sol= | ||
| + | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| + | |||
| + | :sen(x): {{consulta|texto=sin(x)}} {{b4}} cos(x): {{consulta|texto=cos(x)}} {{b4}} tg(x): {{consulta|texto=tan(x)}} | ||
| + | :cosec(x): {{consulta|texto=csc(x)}} {{b4}} sec(x): {{consulta|texto=sec(x)}} {{b4}} cotg(x): {{consulta|texto=cot(x)}} | ||
| + | |||
| + | {{widget generico}} | ||
| + | }} | ||
| + | |||
| + | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]][[Categoría: Funciones]] | [[Categoría: Matemáticas]][[Categoría: Geometría]][[Categoría: Funciones]] | ||
Revisión de 17:33 15 oct 2014
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Vamos a estudiar las funciones que se obtienen a partir de las razones trigonométricas de un ángulo x al hacer variar éste. Dicho ángulo se suele expresar en radianes.
Función seno
Se define la función seno como 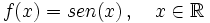 Propiedades de la función seno:
|
Función coseno
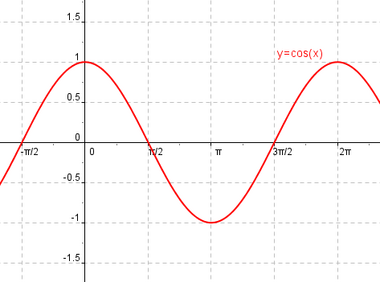
Se define la función coseno como 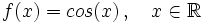 Propiedades de la función coseno:
|
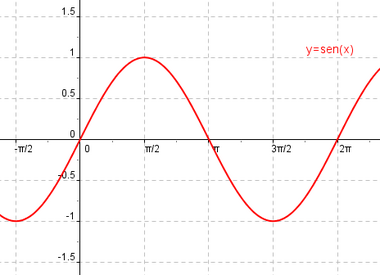
Estudio gráfico de las funciones seno y coseno.
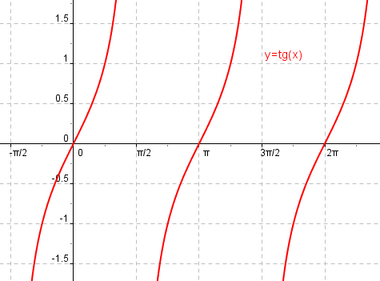
Función tangente
Se define la función coseno como 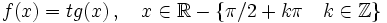 Propiedades de la función tangente:
|
|
Actividad: Funciones trigonométricas
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
![[-1, 1]\,](/wikipedia/images/math/5/8/1/581a26dec23e9f937a02a278e20fc9c3.png)
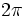 .
.
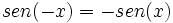
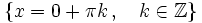
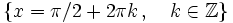
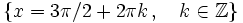
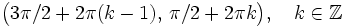 .
.
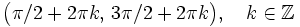 .
.
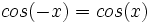
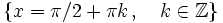
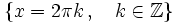
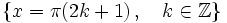
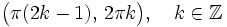 .
.
 .
.
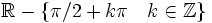
 .
.