Plantilla:Radicales (ampliación)

De Wikipedia

(Diferencia entre revisiones)
Revisión de 18:34 7 ago 2016
Coordinador (Discusión | contribuciones)
(→Caso 2: Denominador con otras raíces)
← Ir a diferencia anterior		 Revisión de 18:35 7 ago 2016
Coordinador (Discusión | contribuciones)
(→Racionalización de denominadores)
Ir a siguiente diferencia →
Línea 95: Línea 95:
{{Caja_Amarilla|texto=Se llama '''racionalización''' al procedimiento por el cual a partir de una fracción con raíces en el denominador obtenemos otra fracción equivalente sin raíces en el denominador}} {{Caja_Amarilla|texto=Se llama '''racionalización''' al procedimiento por el cual a partir de una fracción con raíces en el denominador obtenemos otra fracción equivalente sin raíces en el denominador}}
===Caso 1: Denominador con raíces cuadradas=== ===Caso 1: Denominador con raíces cuadradas===
-Para racionalizar uno de este tipo se debe multiplicar el numerador y el denominador de la fracción por el denominador de la misma.+Para racionalizar uno radical de este tipo se debe multiplicar el numerador y el denominador de la fracción por el denominador de la misma.
{{Ejemplo {{Ejemplo
Línea 119: Línea 119:
===Caso 2: Denominador con otras raíces=== ===Caso 2: Denominador con otras raíces===
-Los exponentes del radicando del radical por el que se deben multiplicar el numerador y denominador de la fracción será la diferencia entre los exponentes actuales y el índice (o múltiplo del indice más cercano) del radical.+En este caso, los exponentes del radicando del radical por el que se deben multiplicar el numerador y denominador de la fracción será la diferencia entre los exponentes actuales y el índice (o múltiplo del indice más cercano) del radical.
{{Ejemplo {{Ejemplo
Línea 139: Línea 139:
===Caso 3: Denominador con sumas y restas de raíces=== ===Caso 3: Denominador con sumas y restas de raíces===
-Se multiplica y divide por la expresión conjugada del denominador (solo se le cambia el segundo signo de la expresión)+Para este último caso, se multiplica y divide por la expresión conjugada del denominador (solo se le cambia el segundo signo de la expresión)
{{Ejemplo {{Ejemplo

Revisión de 18:35 7 ago 2016

Tabla de contenidos

Extracción e introducción de factores en un radical

Extracción de factores

Para extaer factores de un radical se divide el exponente entre el índice y se saca el factor elevado al cociente de la división quedando ese factor elevado al resto.

Ejemplos: 

Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.

Click aquí si no se ve bien la escena

Introducción de factores

Para introducir factores dentro de un radical se multiplica el exponente del factor por el índice del radical.

Ejemplos: 

Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.

Click aquí si no se ve bien la escena

ejercicio

Actividad Interactiva: Introducción y extracción de factores de un radical

Actividad 1. Introduce y extráe factores de radicales.
Actividad:
Pulsa el botón EJERCICIO y verás el enunciado; hazlo en tu cuaderno e introduce la solución con la escena, luego pulsa el botón SOLUCIÓN para ver si lo has hecho bien.
Click aquí si no se ve bien la escena

Suma y resta de radicales con el mismo índice y distinto radicando

Si tienen el mismo índice pero distinto radicando, a veces, podemos extraer factores del radical y dejarlos con el mismo radicando:

Ejemplos: 

Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.

Click aquí si no se ve bien la escena

ejercicio

Actividad Interactiva: Suma y resta de radicales

Actividad 1. Suma y resta radicales con el mismo índice y distinto radicando.
Actividad:
Pulsa el botón EJERCICIO y verás el enunciado; hazlo en tu cuaderno e introduce la solución con la escena, luego pulsa el botón SOLUCIÓN para ver si lo has hecho bien.
Click aquí si no se ve bien la escena
Actividad 2. Operaciones combinadas.
Actividad:

Producto y cocientes de radicales de distinto índice

Para multiplicar o dividir radicales con distintos índices, éstos deben tener el mismo radicando. En tal caso, los radicales los convertimos en potencias de la misma base y operamos con ellas, para obtener una única potencia, que posemos volver a poner en forma radical.

Ejemplos: 
  1. 3\sqrt[3]{5} \cdot \sqrt[4]{5}:\sqrt{5}=3\cdot5^{\frac{1}{3}}\cdot5^{\frac{1}{4}}:5^{\frac{1}{2}}=3\cdot5^{(\frac{1}{3}+\frac{1}{4}-\frac{1}{2})}=3\cdot5^\frac{1}{12}=3\sqrt[12]{5}
  2. 3\sqrt[5]{2}-\sqrt[3]{3}= (No se puede simplificar)

(Otro método: sin pasar a potencia de exponente fraccionario. Ver también: Radicales equivalentes)

Racionalización de denominadores

Se llama racionalización al procedimiento por el cual a partir de una fracción con raíces en el denominador obtenemos otra fracción equivalente sin raíces en el denominador

Caso 1: Denominador con raíces cuadradas

Para racionalizar uno radical de este tipo se debe multiplicar el numerador y el denominador de la fracción por el denominador de la misma.

ejercicio

Ejemplo: Caso 1: Denominador con raíces cuadradas

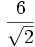
Racionalizar \frac{{6}}{\sqrt{2}}
Solución:

En este caso hay que multiplicar numerador y denominador por 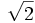\sqrt{2}

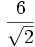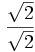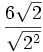
\frac{{6}}{\sqrt{2}} · \frac{\sqrt{2}}{\sqrt{2}} = \frac{{6\sqrt{2}}}{\sqrt{2^2}}


Después se despeja la raíz cuadrada del denominador:

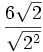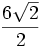
\frac{{6\sqrt{2}}}{\sqrt{2^2}} = \frac{{6\sqrt{2}}}{{2}}


El resultado del ejercicio es éste, aunque se puede simplificar el número entero del numerador entre el del denominador, así:

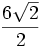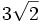
\frac{{6\sqrt{2}}}{{2}} = 3\sqrt{2}

Caso 2: Denominador con otras raíces

En este caso, los exponentes del radicando del radical por el que se deben multiplicar el numerador y denominador de la fracción será la diferencia entre los exponentes actuales y el índice (o múltiplo del indice más cercano) del radical.

ejercicio

Ejemplo: Caso 2: Denominador con otras raíces

Racionalizar \frac{{2}}{\sqrt[5]{a^3b^4}}
Solución:

En este ejemplo, hay que multiplicar por \sqrt[5] {a^2b}, ya que éste es el radical que al ser multiplicado por el denominador los exponentes de las cantidades subradicales serán iguales al índice de la raíz.

Ahora, se procede a multiplicar el numerador y el denominador:

\frac{{2}}{\sqrt[5]{a^3b^4}} · \frac{\sqrt[5] {a^2b} }{\sqrt[5]{a^2b}} = \frac{{2\sqrt[5]{a^2b}}}{\sqrt[5]{a^5b^5}}

Ahora, se procede al despeje de las raíces, en el ejemplo de índice 5:

\frac{{2\sqrt[5]{a^2b}}}{\sqrt[5]{a^5b^5}} = \frac{{2\sqrt[5]{a^2b}}}{{ab}}

Caso 3: Denominador con sumas y restas de raíces

Para este último caso, se multiplica y divide por la expresión conjugada del denominador (solo se le cambia el segundo signo de la expresión)

ejercicio

Ejemplo: Caso 3: Denominador con sumas y restas de raíces

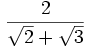
Racionalizar \frac{{2}}{\sqrt{2}+\sqrt{3}}
Solución:

En este caso hay que multiplicar el numerador y el denominador por 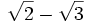{\sqrt{2}-\sqrt{3}}; este resultado es el que da el producto notable de los binomios conjugados.

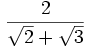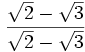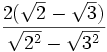
\frac{{2}}{\sqrt{2}+\sqrt{3}} · \frac{{{\sqrt{2}-\sqrt{3}}}}{\sqrt{2}-\sqrt{3}} = \frac{{2({\sqrt{2}-\sqrt{3}}) }}{\sqrt{2^2}-\sqrt{3^2}}

Ahora, se procede al despeje de las raíces cuadradas del denominador:

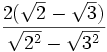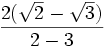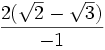\frac{{2({\sqrt{2}-\sqrt{3}}) }}{\sqrt{2^2}-\sqrt{3^2}} = \frac{{2({\sqrt{2}-\sqrt{3}}) }}{{2}-{3}} = \frac{{2({\sqrt{2}-\sqrt{3}}) }}{{-1}} = {-2\sqrt{2}-\sqrt{3}}
Obtenido de "http://www.maralboran.org/wikipedia/index.php/Plantilla:Radicales_%28ampliaci%C3%B3n%29"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda