Plantilla:Término general de la sucesión de Fibonacci

(Diferencia entre revisiones)

Revisión de 13:00 8 sep 2016

Término general de la sucesión de Fibonacci

El término general de la sucesión de Fibonacci es:

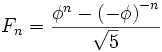
$F_n=\frac{\phi^n-\left(-\phi\right)^{-n}}{\sqrt5}$

siendo 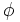$\phi\;$ el número áureo.

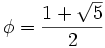
$\phi=\frac{1+\sqrt5}2$

Demostración:

Puedes ver una demostración que sobrepasa este nivel en este enlace: enlace a wikipedia

 {{Teorema|titulo=Término general de la sucesión de Fibonacci
-|enunciado= El término general de la sucesión de Fibonacci es:
+|enunciado=:El término general de la sucesión de Fibonacci es:
 <center><math>F_n=\frac{\phi^n-\left(-\phi\right)^{-n}}{\sqrt5}</math></center>
-siendo <math>\phi\;</math> el número áureo.
+:siendo <math>\phi\;</math> el número áureo.
 <center><math>\phi=\frac{1+\sqrt5}2</math></center>