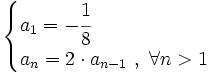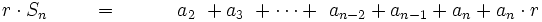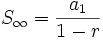Plantilla:Progresiones geométricas

De Wikipedia

(Diferencia entre revisiones)

Revisión de 12:31 14 sep 2016

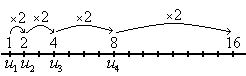
Una progresión geométrica es una sucesión de números en la que cada término se obtiene multiplicando el anterior por una cantidad fija, 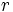$r\;\!$ , que llamaremos razón.

Escrito en forma recursiva:

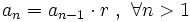
$a_n=a_{n-1} \cdot r \ , \ \forall n>1$

Por ejemplo, la sucesión 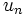$u_n\;$ :

es una progresión geométrica de razón 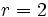$r = 2\;$ .

Progresiones geométricas

Tutorial (5´08") Sinopsis:

Progresiones geométricas: definición y ejemplos.

Ejercicio 1 (3´03") Sinopsis:

Halla el quinto término de la siguiente progresión geométrica: 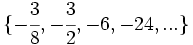$\{ -\cfrac{3}{8}, -\cfrac{3}{2}, -6, -24, ...\}$

Ejercicio 2 (4´31") Sinopsis:

Halla el término 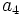$a_4\;$ de una progresión aritmética que viene dada por la siguiente ley de recurrencia:

$\begin{cases}a_1=-\cfrac{1}{8} \\ a_n=2 \cdot a_{n-1} \ , \ \forall n>1 \end{cases}$

Progresiones geométricas

Actividad 1 Descripción:

Actividades en las que aprenderás el concepto de progresión geométrica y a cómo identificarlas.

Autoevaluación 1a Descripción:

Extiende sucesiones geométricas.

Autoevaluación 1b Descripción:

Extiende sucesiones geométricas con términos negativos y racionales.

Autoevaluación 2 Descripción:

Fórmulas recursivas para sucesiones geométricas.

Suma de términos de una progresión geométrica

Suma de términos de una progresión geométrica

La suma de los n primeros términos de una progresión geométrica es:

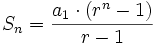
$S_n=\frac{a_1 \cdot(r^n-1)}{r-1}$

Demostración:

Efectuamos la siguiente resta:

$r \cdot S_n \qquad ~= \qquad \quad a_2 \ + a_3 \ + \cdots +\ a_{n-2} + a_{n-1} + a_n +a_n \cdot r$

$-\;$

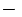
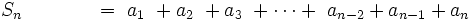
$S_n \ \qquad ~~~~= \ a_1 \ + a_2 \ + a_3 \ + \cdots +\ a_{n-2} + a_{n-1} + a_n$

______________________________________________________________________________

$r \cdot S_n- S_n= -a_1 \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad ~~+a_n \cdot r$

por tanto:

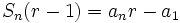
$S_n(r-1)=a_n r-a_1\;$

y despejando

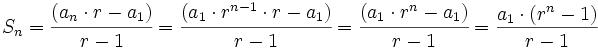
$S_n=\cfrac{(a_n \cdot r - a_1)}{r-1}=\cfrac{(a_1 \cdot r^{n-1} \cdot r - a_1)}{r-1}=\cfrac{(a_1 \cdot r^n - a_1)}{r-1}=\frac{a_1 \cdot(r^n-1)}{r-1}$

Suma de los "n" primeros términos de una progresión geométrica Descripción:

Actividades en las que aprenderás a obtener de los "n" primeros términos de una progresión geométrica.

Suma de términos de una progresión geométrica

Tutorial 1 (3´42") Sinopsis:

Fórmula de la suma de los n primeros términos de una progresión geométrica. Ejemplos.

Tutorial 2 (4'32") Sinopsis:

Fórmula de la suma de los n primeros términos de una progresión geométrica. Ejemplos.

Tutorial 3 (6´48") Sinopsis:

Ejemplos y demostración la fórmula de la suma de n términos consecutivos de una progresión geométrica

Autoevaluación: Suma de los términos de una progresión geométrica Descripción:

Suma los n primeros términos de progresión geométrica dada.

Ejercicio resuelto: Suma de términos de una progresión geométrica

Si al comienzo de cada año ingresamos 1000 € en un banco al 4% anual, ¿cuánto dinero tendremos al final del quinto año?

Solución:

Se trata de un problema típico de aritmética comercial de anualidades de capitalización:

Al comenzar el primer año ingreso 1000 €, que se transforman en 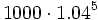$1000 \cdot 1.04^5$ al final del quinto año.

Al comenzar el segundo año ingreso 1000 €, que se transforman en 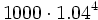$1000 \cdot 1.04^4$ al final del quinto año.

Al comenzar el tercer año ingreso 1000 €, que se transforman en 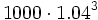$1000 \cdot 1.04^3$ al final del quinto año.

Al comenzar el cuarto año ingreso 1000 €, que se transforman en 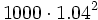$1000 \cdot 1.04^2$ al final del quinto año.

Al comenzar el quinto año ingreso 1000 €, que se transforman en 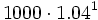$1000 \cdot 1.04^1$ al final del quinto año.

Si sumamos todas esas cantidades:

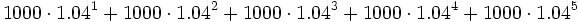
$1000 \cdot 1.04^1 + 1000 \cdot 1.04^2 + 1000 \cdot 1.04^3 + 1000 \cdot 1.04^4 + 1000 \cdot 1.04^5$

estaremos sumando los cinco primeros términos de una progresión geométrica con 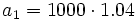$a_1= 1000 \cdot 1.04$ y $r= 1.04\;$

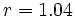
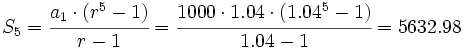$S_5 = \cfrac{a_1 \cdot (r^5 - 1)}{r-1} = \cfrac{1000 \cdot 1.04 \cdot (1.04^5 - 1)}{1.04 -1} = 5632.98$ €

Ejercicios: Anualidades de capitalización Descripción:

Anualidades de capitalización son cantidades fijas que se entregan al principio de cada año para su colocación a interés compuesto con objeto de llegar a constituir un capital al cabo de un determinado número de años.

Ejercicios: Anualidades de amortización Descripción:

Anualidades de amortización son pagos fijos que se entregan al final de cada año para su colocación a interés compuesto, con objeto de llegar a extinguir o amortizar una deuda juntamente con sus intereses, en un determinado número de años.

Suma de los infinitos términos de una progresión geométrica

La suma de todos los términos de una progresión geométrica en la que su razón verifica que 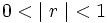$0<\; \mid r \mid \; <1$ se obtiene así:

$S_{\infty}=\frac{a_1}{1-r}$

Demostración:

Para la demostración se requiere del concepto de límite. Véase: Algunos límites importantes.

Producto de términos de una progresión geométrica

Producto de n términos de una progresión geométrica

El producto de los n primeros términos de una progresión geométrica es:

$P_n=\sqrt{(a_1 \cdot a_n)^n}$

Demostración:

Véase en el siguiente videotutorial:

Producto de n términos de una progresión geométrica (7´31") Sinopsis:

Demostración de la fórmula del producto de n términos de una progresión geométrica

Obtenido de "http://www.maralboran.org/wikipedia/index.php/Plantilla:Progresiones_geom%C3%A9tricas"

 {{p}}
 ===Suma de términos de una progresión geométrica===
-{{Teorema
+{{Suma de términos de una progresión geométrica}}
-|titulo=Suma de términos de una progresión geométrica
-|enunciado=
-:La suma de los '''n''' primeros términos de una progresión geométrica es:
-{{p}}
-{{Caja|contenido=<math>S_n=\frac{a_1.r^n-a_1}{r-1}</math>}}
-{{p}}
-|demo=
-Efectuamos la siguiente resta:
-::<math>r \cdot S_n  \qquad ~= \qquad \quad a_2 \ + a_3 \ + \cdots +\ a_{n-2} + a_{n-1} + a_n +a_n \cdot r</math>{{p}}
-:<math>-\;</math>
-::<math>S_n \ \qquad ~~~~= \ a_1 \ + a_2 \ + a_3 \ + \cdots +\ a_{n-2} + a_{n-1} + a_n</math>{{p}}
-::______________________________________________________________________________{{p}}
-::<math>r \cdot S_n- S_n= -a_1 \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad ~~+a_n \cdot r</math>
-por tanto:
-<center><math>S_n(r-1)=a_n r-a_1\;</math></center>
-y despejando
-<center><math>S_n=\cfrac{(a_n \cdot r - a_1)}{r-1}=\cfrac{(a_1 \cdot r^{n-1} \cdot r - a_1)}{r-1}=\cfrac{(a_1 \cdot r^n - a_1)}{r-1}</math></center>
-}}
-{{p}}
-{{Video_enlace
-|titulo1=Suma de n términos consecutivos de una progresión geométrica
-|duracion=6´48"
-|url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/04-sucesiones-aritmeticas-sucesiones-geometricas/07-suma-de-terminos-consecutivos-de-una-sucesion-geometrica#.VCaqh_l_u2E
-|sinopsis=Ejemplos y demostración la fórmula de la suma de n términos consecutivos de una progresión geométrica
-}}
 {{p}}
 {{Teorema

Plantilla:Progresiones geométricas

De Wikipedia

Revisión de 12:31 14 sep 2016

Suma de términos de una progresión geométrica

Producto de términos de una progresión geométrica

Vistas

Herramientas personales

Menú

Buscar

Herramientas