Plantilla:Wolfram Fibonacci
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 12:27 14 ago 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 5: | Línea 5: | ||
| |enunciado= | |enunciado= | ||
| - | :a) ¿Cuál es la sucesión de Fibonacci? | + | a) ¿Cuál es la sucesión de Fibonacci? |
| - | :b) ¿Cual es el término 10 de la sucesión de Fibonacci? | + | |
| - | :c) Escribe los 15 primeros términos de la sucesión de Fibonacci | + | b) ¿Cual es el término 10 de la sucesión de Fibonacci? |
| + | |||
| + | c) Escribe los 15 primeros términos de la sucesión de Fibonacci | ||
| + | |||
| + | d) Comprueba que la sucesión <math>{F_n \over F_{n-1}} \;</math> tiende al número áureo, siendo <math>F_n \;</math> la sucesión de Fibonacci? | ||
| {{p}} | {{p}} | ||
| |sol= | |sol= | ||
| Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| - | :a) {{consulta|texto=Fibonacci sequence}} | + | a) {{consulta|texto=Fibonacci sequence}} |
| - | :b) {{consulta|texto=Fibonacci[10]}} | + | |
| - | :c) {{consulta|texto=Fibonacci[Range[1,15]]}} | + | b) {{consulta|texto=Fibonacci[10]}} |
| + | |||
| + | c) {{consulta|texto=Fibonacci[Range[1,15]]}} | ||
| + | |||
| + | d) {{consulta|texto=limit Fibonacci [n]/Fibonacci [n-1] as n->infinity}} | ||
| {{widget generico}} | {{widget generico}} | ||
Revisión actual
|
Actividad: Sucesión de Fibonacci a) ¿Cuál es la sucesión de Fibonacci? b) ¿Cual es el término 10 de la sucesión de Fibonacci? c) Escribe los 15 primeros términos de la sucesión de Fibonacci d) Comprueba que la sucesión Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: a) Fibonacci sequence b) Fibonacci[10] c) Fibonacci[Range[1,15]] d) limit Fibonacci [n]/Fibonacci [n-1] as n->infinity |
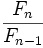 tiende al número áureo, siendo
tiende al número áureo, siendo 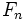 la sucesión de Fibonacci?
la sucesión de Fibonacci?

