Resolución de triángulos rectángulos (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:58 19 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 12:46 23 nov 2016 Coordinador (Discusión | contribuciones) (→Resolución de triángulos rectángulos) Ir a siguiente diferencia → |
||
| Línea 38: | Línea 38: | ||
| :Hallamos el cateto {{sube|porcentaje=10%|contenido=<math>a: \quad cos \ \hat B=\cfrac{a}{c} \rightarrow c=\cfrac{a}{cos \, \hat B}=\cfrac{15}{cos \, 50^\circ}=23.34 \, cm</math>}} | :Hallamos el cateto {{sube|porcentaje=10%|contenido=<math>a: \quad cos \ \hat B=\cfrac{a}{c} \rightarrow c=\cfrac{a}{cos \, \hat B}=\cfrac{15}{cos \, 50^\circ}=23.34 \, cm</math>}} | ||
| : Hallamos el ángulo {{sube|porcentaje=15%|contenido=<math>\hat A: \quad \hat A= 90^\circ - \hat B=90^\circ - 50^\circ=40^\circ</math>}} | : Hallamos el ángulo {{sube|porcentaje=15%|contenido=<math>\hat A: \quad \hat A= 90^\circ - \hat B=90^\circ - 50^\circ=40^\circ</math>}} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=En esta escena podrás ver como se calculan alturas de objetos cuya base es accesible. | ||
| + | |enlace=[https://ggbm.at/KwbbuWEX Calcula la altura de un edificio cuya base es accesible] | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 84: | Línea 89: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Ejercicios propuestos== | ==Ejercicios propuestos== | ||
| {{ejercicio | {{ejercicio | ||
Revisión de 12:46 23 nov 2016
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 112)
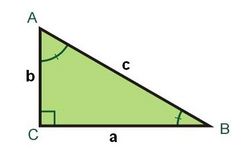
Resolución de triángulos rectángulos
Resolver un triángulo es hallar los lados y ángulos desconocidos a partir de los conocidos.
Resolución de triángulos rectángulos
- Caso 1: Nos dan 2 lados:
- El lado que falta se halla por el teorema de Pitágoras.
- El ángulo que forman los lados conocidos se halla mediante la razón trigonométrica que los relaciona.
- Caso 2: Nos dan 1 lado y 1 ángulo agudo:
- Uno de los lados se halla mediante la razón trigonométrica que lo relaciona con el lado y el ángulo conocidos.
- El otro ángulo agudo se halla como complementario del que nos dan.
Ejemplos: Resolución de triángulos rectángulos
- Caso 1: Resuelve un triángulo rectángulo del que nos dan un cateto que mide 11 cm y la hipotenusa que mide 20 cm.
- Caso 2: Resuelve un triángulo rectángulo del que nos dan un cateto que mide 15 cm y su ángulo contiguo que mide 50º.
Solución:
- Caso 1:
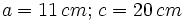
- Hallamos el cateto
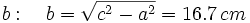(Por el teorema de Pitágoras)
- Hallamos el ángulo
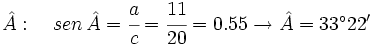
- Hallamos el ángulo
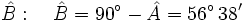
- Caso 2:
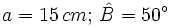
- Hallamos el cateto
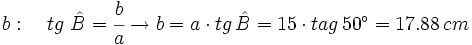
- Hallamos el cateto
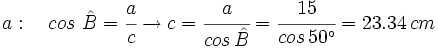
- Hallamos el ángulo
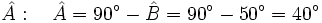
En esta escena podrás ver como se calculan alturas de objetos cuya base es accesible.
- Si pulsas el botón "EJERCICIO" cambiarán los datos del problema resuelto.
- Si pulsas el botón "AUTOEVALUACIÓN" podrás realizar una tanda de ejercicios para comprobar lo que sabes.
- Si pulsas el botón "EJERCICIO" cambiarán los datos del problema resuelto.
Resolución de triángulos rectángulos (8´43") Sinopsis: - Resolver un triángulo es identificarlo; o sea, determinar sus lados y ángulos. Para resolver un triángulo rectángulo basta conocer, además del ángulo recto, un ángulo y un lado o dos de los lados.
- Ejemplos.
3 ejercicios (5´41") Sinopsis: - Resuelve el triángulo rectángulo cuyos catetos miden 6 y 8 cm.
- Resuelve el triángulo rectángulo cuyo cateto mide 8 cm y su ángulo adyacente 60º.
- Determina la sombra proyectada por un árbol de 10 m de altura cuando el sol levanta 30º sobre el horizonte.
Ejercicios propuestos
 Ejercicios propuestos: Resolución de triángulos rectángulos (Pág. 113)
|
