Plantilla:Transformaciones elementales de funciones (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 20:02 12 dic 2016 Coordinador (Discusión | contribuciones) (→Dilatación y contracción) ← Ir a diferencia anterior |
Revisión de 20:04 12 dic 2016 Coordinador (Discusión | contribuciones) (→Dilatación y contracción) Ir a siguiente diferencia → |
||
| Línea 26: | Línea 26: | ||
| '''Vertical:''' | '''Vertical:''' | ||
| - | *Si <math>k>1\;</math>, la gráfica de la función <math>k \cdot f(x)\;</math> es una '''dilatación''' o estiramiento vertical de la gráfica de <math>f(x)\;</math>. | + | *Si <math>k>1\;</math>, la gráfica de la función <math>k \cdot f(x)\;</math> es una '''dilatación vertical''' de la gráfica de <math>f(x)\;</math>. |
| - | *Si <math>0<k<1\;</math>, la gráfica de la función <math>k \cdot f(x)\;</math> es una '''contracción''' o achatamiento vertical de la gráfica de <math>f(x)\;</math>. | + | *Si <math>0<k<1\;</math>, la gráfica de la función <math>k \cdot f(x)\;</math> es una '''contracción vertical''' vertical de la gráfica de <math>f(x)\;</math>. |
| '''Horizontal:''' | '''Horizontal:''' | ||
| - | *Si <math>k>1\;</math>, la gráfica de la función <math>f(k \cdot x)\;</math> es una '''contracción''' o estrechamiento horizontal de la gráfica de <math>f(x)\;</math>. | + | *Si <math>k>1\;</math>, la gráfica de la función <math>f(k \cdot x)\;</math> es una '''contracción horizontal''' de la gráfica de <math>f(x)\;</math>. |
| - | *Si <math>0<k<1\;</math>, la gráfica de la función <math>f(k \cdot x)\;</math> es una '''dilatación''' o ensanchamiento horizontal de la gráfica de <math>f(x)\;</math>. | + | *Si <math>0<k<1\;</math>, la gráfica de la función <math>f(k \cdot x)\;</math> es una '''dilatación horizontal''' de la gráfica de <math>f(x)\;</math>. |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 20:04 12 dic 2016
Tabla de contenidos |
Traslación vertical y horizontal
- Traslación vertical: Sea
 una función y
una función y 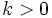 un número real, entonces la gráfica de la función
un número real, entonces la gráfica de la función 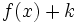 se obtiene a partir de la de
se obtiene a partir de la de  desplazándola
desplazándola 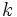 unidades hacia arriba y la de
unidades hacia arriba y la de 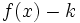 desplazándola
desplazándola 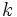 unidades hacia abajo.
unidades hacia abajo.
- Traslación horizontal: Sea
 una función y
una función y 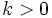 un número real, entonces la gráfica de la función
un número real, entonces la gráfica de la función 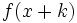 se obtiene a partir de la de
se obtiene a partir de la de  desplazándola
desplazándola 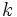 unidades hacia la izquierda y la de
unidades hacia la izquierda y la de 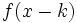 desplazándola
desplazándola 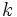 unidades hacia la derecha.
unidades hacia la derecha.
En esta escena podrás ver la representación conjunta una función y su transformada por traslación horizontal o vertical.
Simetrías
- Simetría respecto del eje X: Las gráficas de las funciones
 y
y 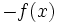 son simétricas respecto del eje de abscisas.
son simétricas respecto del eje de abscisas.
- Simetría respecto del eje Y: Las gráficas de las funciones
 y
y 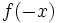 son simétricas respecto del eje de ordenadas.
son simétricas respecto del eje de ordenadas.
- Simetría respecto del origen: Las gráficas de las funciones
 y
y 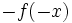 son simétricas respecto del origen de coordenadas.
son simétricas respecto del origen de coordenadas.
En esta escena podrás ver la representación conjunta una función y su simétrica.
Dilatación y contracción
Vertical:
- Si
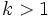 , la gráfica de la función
, la gráfica de la función 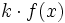 es una dilatación vertical de la gráfica de
es una dilatación vertical de la gráfica de  .
.
- Si
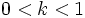 , la gráfica de la función
, la gráfica de la función 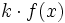 es una contracción vertical vertical de la gráfica de
es una contracción vertical vertical de la gráfica de  .
.
Horizontal:
- Si
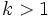 , la gráfica de la función
, la gráfica de la función 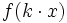 es una contracción horizontal de la gráfica de
es una contracción horizontal de la gráfica de  .
.
- Si
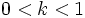 , la gráfica de la función
, la gráfica de la función 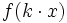 es una dilatación horizontal de la gráfica de
es una dilatación horizontal de la gráfica de  .
.
En esta escena podrás ver la representación conjunta una función y su transformada por dilatación o contracción.
Actividades
En esta escena podrás practicar las transformaciones de funciones. Se te propondrán algunos ejercicios.

