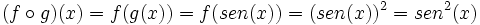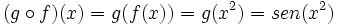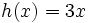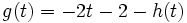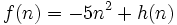Composición de funciones (1ºBach)
De Wikipedia
| Revisión de 17:52 23 ene 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Ejercicios propuestos) |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | ==Función compuesta== | + | __TOC__ |
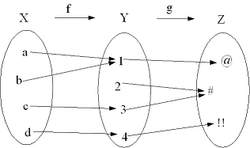
| - | [[Imagen:Compfun.png|250px|thumb|''g'' <small>o</small> ''f'', es la aplicación resultante de la aplicación sucesiva de'' f'' y de ''g''. En el ejemplo, (''g'' <small>o</small> ''f'')(a)=@.]] | + | {{p}} |
| - | En [[matemática]], una '''función compuesta''' es una [[Función matemática|función]] formada por la [[Operación matemática|composición]] o aplicación sucesiva de otras dos funciones. Para ello, se aplica sobre el argumento la función más próxima al mismo, y al resultado del cálculo anterior se le aplica finalmente la función restante. | + | (Pág. 258) |
| + | {{p}} | ||
| + | {{Composición de funciones (1ºBach)}} | ||
| + | {{p}} | ||
| + | ==Ejercicios propuestos== | ||
| + | {{ejercicio | ||
| + | |titulo=Ejercicios propuestos: ''Composición de funciones'' | ||
| + | |cuerpo= | ||
| + | (Pág. 258) | ||
| - | Formalmente, dadas dos funciones ''f: X → Y'' y ''g: Y → Z'', donde la [[imagen]] de ''f'' está contenida en el [[dominio de definición|dominio]] de ''g'', se define la función composición '''(''g'' ο ''f'' ): ''X'' → ''Z''''' como '''(''g'' ο ''f'')(''x'') = ''g'' (''f''(''x''))''', para todos los elementos ''x'' de ''X''. | + | [[Imagen:red_star.png|12px]] 1, 2 |
| - | :::::::<math>X \to \,\,Y\;\; \to \;\;\,Z</math> | + | |
| - | :::::::<math>x \mapsto f(x) \mapsto g(f(x))</math> | + | |
| - | + | ||
| - | A ''g'' ο ''f'' se le llama ''composición de f y g''. Nótese que se nombra no siguiendo el orden de escritura, sino el orden en que se aplican las funciones a su argumento. | + | |
| - | == Ejemplo == | + | |
| - | Sean las funciones: | + | |
| - | : <math> f(x) = x^2 \,</math> | + | |
| - | : <math> g(x) = sin(x) \,</math> | + | |
| - | + | ||
| - | La '''función compuesta''' de ''g'' y de ''f'' que expresamos: | + | |
| - | : <math> (f \circ g)(x) = f(g(x)) = (sin(x))^2 = sin^2 (x) \,</math> | + | |
| - | + | ||
| - | La interpretación de (''f'' o ''g'') aplicada a la variable ''x'' significa que primero tenemos que aplicar ''g'' a ''x'', con lo que obtendríamos un valor de paso | + | |
| - | : <math> z = g(x)=sin(x) \, </math> | + | |
| - | + | ||
| - | y después aplicamos ''f'' a ''z'' para obtener | + | |
| - | : <math> y = f(z) = z^2 = sin^2(x) \, </math> | + | |
| + | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Funciones]] | [[Categoría: Matemáticas]][[Categoría: Funciones]] | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 258)
Función compuesta
| La función compuesta es una función formada por la aplicación sucesiva de otras dos funciones. Formalmente:
Dadas dos funciones 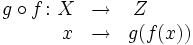 Se aplica sobre el argumento la función más próxima al mismo, y al resultado del cálculo anterior se le aplica finalmente la función restante. 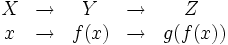 La expresión |
En esta escena analizaremos gráficamente como se obtiene la composición de dos funciones.
Ejemplo: Composición de funciones
Dadas las funciones: 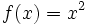 y
y 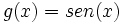
- a) Halla la función
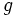 compuesta con
compuesta con 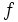 .
.
- b) Halla la función
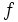 compuesta con
compuesta con 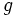 .
.
a) La función 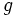 compuesta con
compuesta con 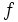 es:
es:
b) La función 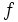 compuesta con
compuesta con 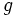 es:
es:
Utiliza la siguiente escena para representar las funciones que acabamos de componer en el ejemplo anterior.
En esta escena podrás ver representadas, de forma conjunta, dos funciones y sus compuestas.
Introducción a la composición de funciones
Introducción a la composición de funciones
Tutorial dedicado a las operaciones con funciones. En este caso la composición de funciones (f o g)(x)
Introducción al concepto de composición o encadenamiento de funciones.
Halla la composición 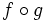 y
y 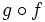 de las funciones
de las funciones 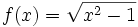 y
y 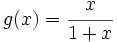
Halla la composición 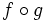 y
y 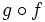 de las funciones
de las funciones 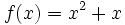 y
y 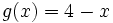
Evaluar funciones compuestas usando tablas
Dadas las funciones:
calcula 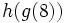 .
.
Evaluar funciones compuestas usando gráficas
4 ejercicios sobre composición de funciones
Halla 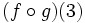 y
y 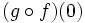 de las funciones
de las funciones 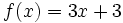 y
y 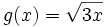
Halla 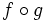 ,
, 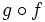 ,
, 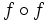 y
y 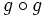 de las funciones
de las funciones 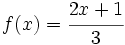 y
y 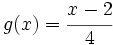
Halla 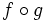 y
y 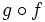 de las funciones
de las funciones 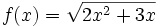 y
y 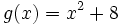
Halla 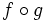 y
y 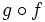 de las funciones
de las funciones 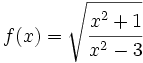 y
y 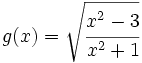
Halla 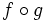 ,
, 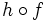 ,
, 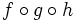 ,
, 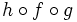 y
y 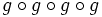 de las funciones
de las funciones 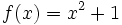 ,
, 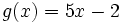 y
y 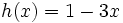
4 ejercicios sobre composición de funciones
Ejercicio sobre la composición de 3 funciones
3 ejercicios sobre composición de 3 funciones
Este videotutorial te será útil, en especial, para cuando veamos la regla de la cadena en el tema de derivadas.
Este videotutorial te acercará la composición de funciones a modelos prácticos.
Ejercicios propuestos
|
Ejercicios propuestos: Composición de funciones |
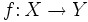 y
y 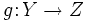 , donde la imagen de
, donde la imagen de 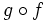 se lee f compuesta con g. Nótese que se nombra, no siguiendo el orden de escritura, sino el orden en que se aplican las funciones a su argumento.
se lee f compuesta con g. Nótese que se nombra, no siguiendo el orden de escritura, sino el orden en que se aplican las funciones a su argumento.