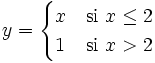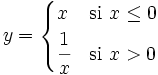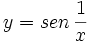Plantilla:Límite de una función (1ºBach)
De Wikipedia
| Revisión de 11:44 18 dic 2016 Coordinador (Discusión | contribuciones) (→Límite de de una función en un punto) ← Ir a diferencia anterior |
Revisión de 11:53 18 dic 2016 Coordinador (Discusión | contribuciones) (→Límite de de una función en un punto) Ir a siguiente diferencia → |
||
| Línea 73: | Línea 73: | ||
| |titulo1=Funciones sin límite en un punto | |titulo1=Funciones sin límite en un punto | ||
| |duracion=17'06" | |duracion=17'06" | ||
| - | |sinopsis=Sólo tiene sentido calcular los límites laterales de una función en un punto cuando la función está definida en las "proximidades" del punto | + | |sinopsis=Sólo tiene sentido calcular los límites laterales de una función en un punto cuando la función está definida en las "proximidades" del punto. |
| + | |||
| + | '''AVISO:''' Este video excede, en parte, el nivel de 1º de bachillerato. | ||
| |url1=http://matematicasbachiller.com/videos/universidad/calculo-diferencial-de-una-variable/02-limites-de-funciones/09-funciones-sin-limite-en-un-punto | |url1=http://matematicasbachiller.com/videos/universidad/calculo-diferencial-de-una-variable/02-limites-de-funciones/09-funciones-sin-limite-en-un-punto | ||
| }} | }} | ||
Revisión de 11:53 18 dic 2016
Tabla de contenidos |
Límite de de una función en un punto
El concepto de límite es la base para poder abordar el concepto de continuidad y , más adelante, el de derivabilidad de una función. Es pués, de vital interés, tener bien claro este concepto.
- Decimos que "
 tiende a
tiende a  por la izquierda" (
por la izquierda" (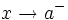 ) cuando
) cuando  toma valores menores que
toma valores menores que  , cada vez más próximos a
, cada vez más próximos a  .
.
- Decimos que "
 tiende a
tiende a  por la derecha" (
por la derecha" (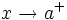 ) cuando
) cuando  toma valores mayores que
toma valores mayores que  , cada vez más próximos a
, cada vez más próximos a  .
.
- Decimos que "
 tiende a
tiende a  " (
" ( ) cuando
) cuando  toma valores cada vez más próximos a
toma valores cada vez más próximos a  .
.
La clave para entender el Cálculo Diferencial de una variable y divertirse con él es aprender a "meterse en la piel" de un habitante genérico "x" de la recta real. En este vídeo describimos la vida de "x" ("x" eres tú) en el alambre infinito donde vive: un universo de una única dimensión.
- Los puntos en la recta real.
- Aproximación a un punto por la derecha y por la izquierda.
- Aproximación a
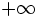 y
y 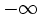 .
.
- Concepto de distancia entre dos puntos.
- Concepto de entorno de un punto.
- Aproximación a un punto por la derecha y por la izquierda.
- Aproximación a
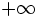 y
y 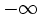 .
.
Dada una función  , cuando la variable independiente
, cuando la variable independiente  se aproxima a un cierto punto
se aproxima a un cierto punto  , ya sea por la derecha o por la izquierda,
, ya sea por la derecha o por la izquierda,  va tomando valores que pueden aproximarse o no a un cierto punto. Diremos que:
va tomando valores que pueden aproximarse o no a un cierto punto. Diremos que:
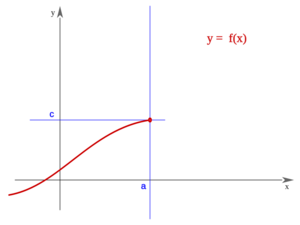
- Una función
 tiene límite por la izquierda en un punto
tiene límite por la izquierda en un punto  , si existe un número
, si existe un número 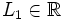 , de manera que cuando
, de manera que cuando 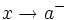 , los correspondientes valores
, los correspondientes valores 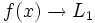 . Lo representaremos:
. Lo representaremos:
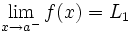
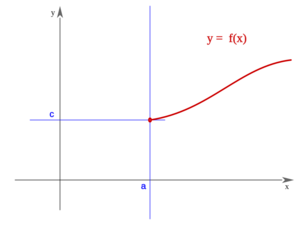
- Una función
 tiene límite por la derecha en un punto
tiene límite por la derecha en un punto  , si existe un número
, si existe un número 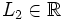 , de manera que cuando
, de manera que cuando 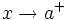 , los correspondientes valores
, los correspondientes valores 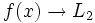 . Lo representaremos:
. Lo representaremos:
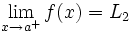
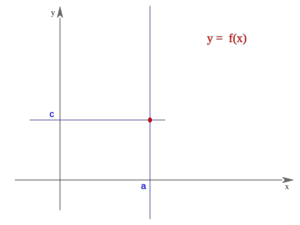
- Una función
 tiene límite en un punto
tiene límite en un punto  , si existe un número
, si existe un número 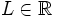 de manera que
de manera que
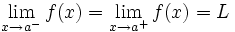
y lo representaremos:
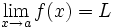
Nótese que aunque existan los límites laterales, si estos no coinciden, el límite no existe.
En este vídeo, el más importante de todos, hablamos del mágico instante en que tú, el número real "x", por amor, consagras gozosamente tu existencia a la observación y análisis de la Dulcinea "f(x)" que da sentido a tu vida y la llena de alegría y diversión.
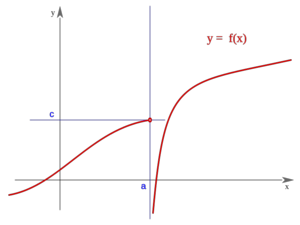
En este vídeo hablamos de los dos límites laterales de una función "f" en un punto "a" (límite de "f" en "a" por la izquierda y límite de "f" en "a" por la derecha), interpretándolos en términos geométricos. Si dichos dos límites laterales de "f" en "a" son iguales a "L", se dice que "L" es el límite de "f" en "a".
- Conceptos de límite de una función por la derecha y por la izquierda de un punto.
- Concepto de límite de una función en un punto.
- Se puede calcular el límite en un punto independientemente de que el punto pertenezca o no al dominio de la función. Ejemplos.
Sólo tiene sentido calcular los límites laterales de una función en un punto cuando la función está definida en las "proximidades" del punto.
AVISO: Este video excede, en parte, el nivel de 1º de bachillerato.
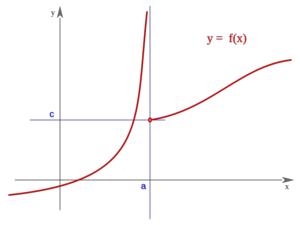
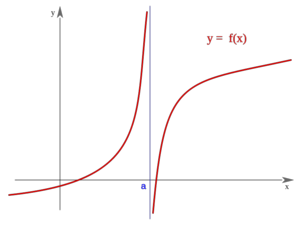
Límites infinitos. Asíntotas verticales
El concepto de límite visto en el apartado anterior puede extenderese al caso en que, al aproximarnos al punto  , la función se aproxime a
, la función se aproxime a 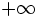 ó
ó 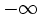 .
.
- Una función
 tiende a
tiende a 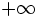 por la izquierda de un punto
por la izquierda de un punto  , si
, si  se aproxima a valores positivos cada vez más grandes y no acotables, cuando
se aproxima a valores positivos cada vez más grandes y no acotables, cuando 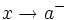 . Lo representaremos:
. Lo representaremos:
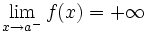
- Una función
 tiende a
tiende a 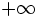 por la derecha de un punto
por la derecha de un punto 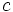 , si
, si  se aproxima a valores positivos cada vez más grandes y no acotables, cuando
se aproxima a valores positivos cada vez más grandes y no acotables, cuando 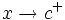 . Lo representaremos:
. Lo representaremos:
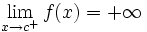
- Una función
 tiende a
tiende a 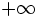 en un punto
en un punto 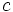 , si
, si
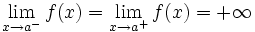
y lo representaremos:
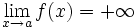
- De forma análoga se puede definir la tendencia a
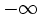 si cambiamos la frase "se aproxima a valores positivos cada vez más grandes y no acotables" por "se aproxima a valores negativos cada vez más pequeños y no acotables", en los tres casos.
si cambiamos la frase "se aproxima a valores positivos cada vez más grandes y no acotables" por "se aproxima a valores negativos cada vez más pequeños y no acotables", en los tres casos.
- En todos estos casos diremos que la función tiene una asíntota vertical en el punto
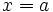 .
.
En este vídeo definimos el concepto de límite infinito de una función en un punto y lo interpretamos geométricamente: asíntotas verticales.
Ejercicios propuestos
|
Ejercicios propuestos: Límite de una función en un punto |
Continuidad de una función en un punto
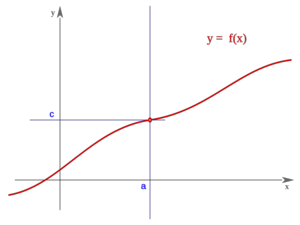
Una función  es continua en un punto
es continua en un punto  , si se cumple que:
, si se cumple que:
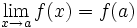
Para que ésto se cumpla deben ocurrir las tres condiciones siguientes:
- La función
 tiene límite en
tiene límite en 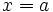 :
: 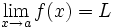
- La función está definida en
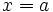 : Existe
: Existe 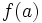
- Los dos valores anteriores coinciden:
La función "f" se dice continua por la izquierda (derecha) en el punto "a" si el límite de "f" en "a" por la izquierda (derecha) es finito y coincide con f(a). Se dice que "f" es continua en "a" si es continua por la izquierda y por la derecha en "a".
Video tutorial de matematicasbachiller.com
Tipos de discontinuidades
Discontinuidad evitable
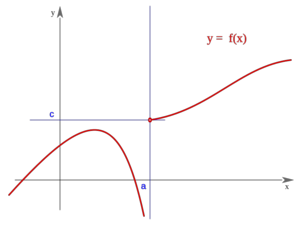
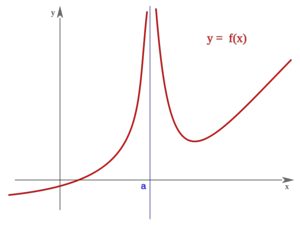
Una función  tiene una discontinuidad evitable en un punto
tiene una discontinuidad evitable en un punto 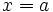 si existe
si existe 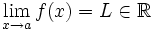 pero éste no coincide con
pero éste no coincide con 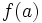 , bien porque
, bien porque  no esté definida en
no esté definida en 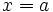 o bien porque simplemente sean distintos.
o bien porque simplemente sean distintos.
Evitable (no definida en un punto, tiene un hueco)
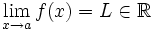 , pero , pero 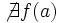 | Evitable (punto desplazado que deja un hueco)
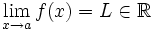 , pero , pero 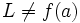 |
Ejemplo: Discontinuidad evitable
Comprueba en qué puntos presentan las siguientes funciones una discontinuidad evitable:
- a)
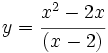 b)
b) 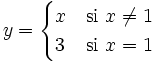
a) En x=2 tiene una discontinuidad evitable.
b) En x=2 tiene una discontinuidad evitable.
Puedes hacer uso de la siguiente escena de Geogebra para comprobar las soluciones:
En esta escena podrás representar funciones definidas en hasta 4 trozos.
La función "f" presenta "discontinuidad evitable" en el punto "a" si tiene límite finito en "a" pero no coincide con f(a). El términos geométricos significa que la gráfica de "f" tiene un "agujerito" en "a". Se "evita" la discontinuidad "rellenando" el agujerito; y para ello basta redefinir "f" de modo que f(a) coincida con el límite de "f" en "a".
Ejemplos: Discontinuidad evitable
Discontinuidad esencial de primera especie
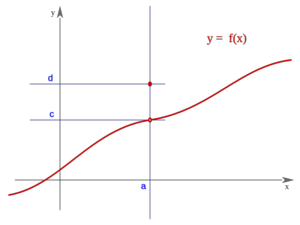
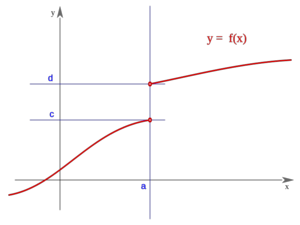
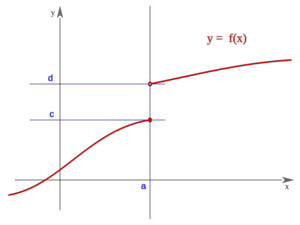
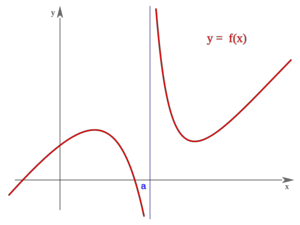
Una función  tiene una discontinuidad esencial de primera especie de salto finito en un punto
tiene una discontinuidad esencial de primera especie de salto finito en un punto 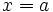 si existen los límites laterales en dicho punto y son finitos, pero estos no coinciden:
si existen los límites laterales en dicho punto y son finitos, pero estos no coinciden:
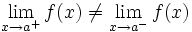
Se llama salto al valor absoluto de la diferencia enter ambos límites:
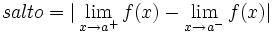
Nota: 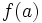 puede estar definida o no, y puede coincidir o no con uno de los dos límites laterales.
puede estar definida o no, y puede coincidir o no con uno de los dos límites laterales.
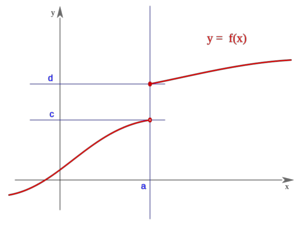
Salto finito (Salto=d-c)
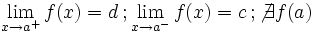 | Salto finito (Salto=d-c)
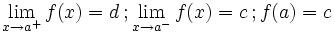 |
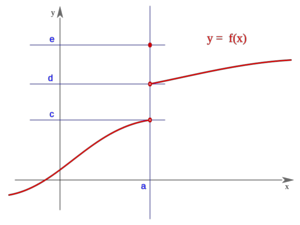
Salto finito (Salto=d-c)
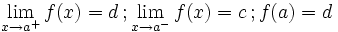 | Salto finito (Salto=d-c)
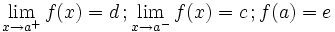 |
Ejemplo: Discontinuidad de salto finito
Comprueba en qué punto presenta la siguiente función una discontinuidad de salto finito y averigua el valor del salto:
En x=2 tiene una discontinuidad de salto finito. El salto es igual a | 2 − 1 | = 1.
Puedes hacer uso de la siguiente escena de Geogebra para comprobar la solución:
En esta escena podrás representar funciones definidas en hasta 4 trozos.
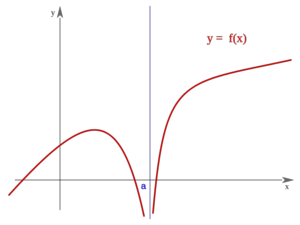
Una función  tiene una discontinuidad esencial de primera especie de salto infinito si existen los límites laterales, siendo uno finito y otro infinito.
tiene una discontinuidad esencial de primera especie de salto infinito si existen los límites laterales, siendo uno finito y otro infinito.
Nota: 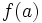 puede estar definida o no, y puede coincidir o no con el límite lateral finito.
puede estar definida o no, y puede coincidir o no con el límite lateral finito.
Salto infinito
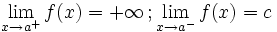 En este caso "f(a)" no está definida pero podría estarlo y coincidir o no con "c" En este caso "f(a)" no está definida pero podría estarlo y coincidir o no con "c" | Salto infinito
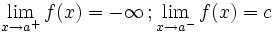 En este caso "f(a)" no está definida pero podría estarlo y coincidir o no con "c" En este caso "f(a)" no está definida pero podría estarlo y coincidir o no con "c" |
Salto infinito
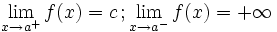 En este caso "f(a)" no está definida pero podría estarlo y coincidir o no con "c" En este caso "f(a)" no está definida pero podría estarlo y coincidir o no con "c" | Salto infinito
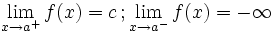 En este caso "f(a)" no está definida pero podría estarlo y coincidir o no con "c" En este caso "f(a)" no está definida pero podría estarlo y coincidir o no con "c" |
Ejemplo: Discontinuidad de salto infinito
Comprueba en qué punto presenta la siguiente función una discontinuidad de salto ifinito:
En x=0 tiene una discontinuidad de salto infinito.
Puedes hacer uso de la siguiente escena de Geogebra para comprobar la solución:
En esta escena podrás representar funciones definidas en hasta 4 trozos.
Una función  tiene una discontinuidad esencial de primera especie asintótica si si existen los límites laterales, siendo ambos + o - infinito, pero no necesariamente iguales.
tiene una discontinuidad esencial de primera especie asintótica si si existen los límites laterales, siendo ambos + o - infinito, pero no necesariamente iguales.
Nota: 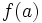 puede estar definida o no.
puede estar definida o no.
Asintótica
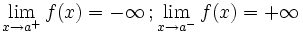 En este caso "f(a)" no está definida pero podría estarlo En este caso "f(a)" no está definida pero podría estarlo | Asintótica
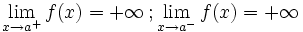 En este caso "f(a)" no está definida pero podría estarlo En este caso "f(a)" no está definida pero podría estarlo |
Asintótica
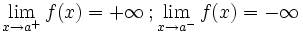 En este caso "f(a)" no está definida pero podría estarlo En este caso "f(a)" no está definida pero podría estarlo | Asintótica
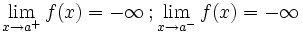 En este caso "f(a)" no está definida pero podría estarlo En este caso "f(a)" no está definida pero podría estarlo |
Ejemplo: Discontinuidad asintótica
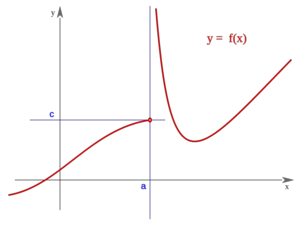
Comprueba en qué puntos presentan las siguientes funciones una discontinuidad asintótica:
- a)
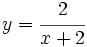 b)
b) 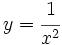
a) En x=-2 tiene una discontinuidad asintótica.
b) En x=0 tiene una discontinuidad asintótica.
Puedes hacer uso de la siguiente escena de Geogebra para comprobar la solución:
En esta escena podrás representar funciones definidas en hasta 4 trozos.
La función "f" presenta "discontinuidad de primera especie" en el punto "a" si los límites laterales de "f" en "a" son distintos. El términos geométricos significa que la gráfica de "f" da un "salto" en "a".
Ejemplos: Discontinuidad de primera especie
3 ejercicios sobre discontinuidades de primera especie
3 ejercicios sobre discontinuidades de primera especie
Discontinuidad esencial de segunda especie
Una función  tiene una discontinuidad de segunda especie si no existe alguno de los límites laterales.
tiene una discontinuidad de segunda especie si no existe alguno de los límites laterales.
Nota: 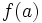 puede estar definida o no.
puede estar definida o no.
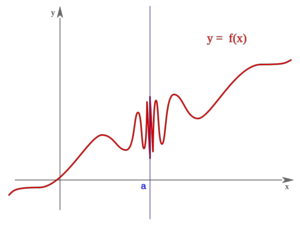
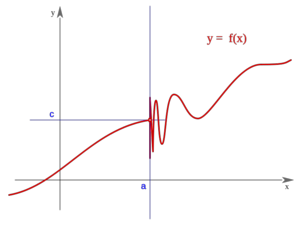
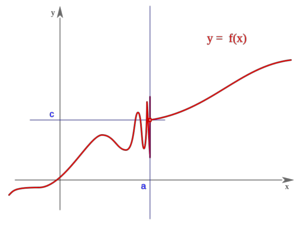
Segunda especie
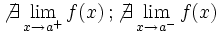 Es oscilante por ambos lados"f(a)" puede estar definida o no Es oscilante por ambos lados"f(a)" puede estar definida o no | Segunda especie
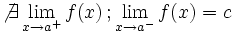 Es oscilante por la derecha"f(a)" puede estar definida o no Es oscilante por la derecha"f(a)" puede estar definida o no | Segunda especie
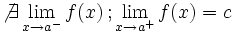 Es oscilante por la izquierda"f(a)" puede estar definida o no Es oscilante por la izquierda"f(a)" puede estar definida o no |
Ejemplo: Discontinuidad de segunda especie
Comprueba en qué punto presenta la siguiente función una discontinuidad de segunda especie:
En x=0 tiene una discontinuidad de segunda especie.
Puedes hacer uso de la siguiente escena de Geogebra para comprobar la solución:
En esta escena podrás representar funciones definidas en hasta 4 trozos.
Algunos autores incluyen dentro de este tipo de discontinuidades los siguientes casos:
No hay función a la derecha de a
| No hay función a la izquierda de a
| No hay función ni a la derecha ni a la izquierda de a
|
No obstante, nosotros supondremos que en los casos en que no exista función por uno de los lados del punto, no tiene sentido hablar de límite lateral por ese lado del punto, y por tanto no diremos que haya discontinuidad por ese lado. (¡Ojo!, si podría haber discontinuidad por el otro lado del punto siempre que tenga sentido hablar de límite lateral por ese otro lado)
Como ejemplo de esto que estamos diciendo tienes el siguiente video:
La función "f" presenta "discontinuidad de segunda especie" en el punto "c" si no existe alguno de los límites laterales de "f" en "c".