Plantilla:Reglas de derivación (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 07:59 16 ene 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 08:13 16 ene 2017 Coordinador (Discusión | contribuciones) (→Derivada de las funciones elementales) Ir a siguiente diferencia → |
||
| Línea 19: | Línea 19: | ||
| ::<math>D(arc\,tg\,x)=\cfrac{1}{1+x^2}</math> | ::<math>D(arc\,tg\,x)=\cfrac{1}{1+x^2}</math> | ||
| + | *'''Funciones exponenciales y logarítmicas:''' | ||
| + | ::<math>D(e^x)=e^x\;</math> | ||
| + | ::<math>D(a^x)=a^x \cdot ln\,a</math> | ||
| + | ::<math>D(ln\,x)=\cfrac{1}{x}</math> | ||
| + | ::<math>D(log_a\,x)=\cfrac{1}{x} \cdot \cfrac{1}{ln\,a}</math> | ||
| + | }} | ||
| + | {{p}} | ||
| + | ==Derivada de operaciones con funciones== | ||
| + | {{Teorema_sin_demo|titulo=Reglas de derivación|enunciado= | ||
| + | *'''Producto de una función por una constante:''' | ||
| + | ::<math>D[k\,f(x)]=k\,f'(x)\;</math> | ||
| + | *'''Suma de funciones:''' | ||
| + | ::<math>D[f(x)+g(x)]=f'(x)+g'(x)\;</math> | ||
| + | *'''Producto de funciones:''' | ||
| + | ::<math>D[f(x) \cdot g(x)]=f'(x) \cdot g(x) + f(x) \cdot g'(x)\;</math> | ||
| + | *'''Cociente de funciones:''' | ||
| + | ::<math>D[\cfrac{f(x)}{g(x)}]=\cfrac{f'(x) \cdot g(x) + f(x) \cdot g'(x)}{g(x)^2}\;</math> | ||
| + | *'''Composición de funciones (Regla de la cadena):''' | ||
| + | ::<math>D{g[f(x)]}=g'[f(x)] \cdot f'(x)\;</math> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 08:13 16 ene 2017
Hemos visto en el apartado anterior como se obtiene la Función derivada de una función. Es un proceso largo y pesado. Existen una serie de reglas, demostradas por medio de ese procedimiento, que nos permitirán aliviar el trabajo del cálculo de la función derivada.
Derivada de las funciones elementales
Reglas de derivación
- Función constante:
- Función identidad:
- Función potencia:
- Funciones trigonométricas directas:
- Funciones trigonométricas recíprocas:
- Funciones exponenciales y logarítmicas:
Derivada de operaciones con funciones
Reglas de derivación
- Producto de una función por una constante:
- Suma de funciones:
- Producto de funciones:
- Cociente de funciones:
- Composición de funciones (Regla de la cadena):
Definición de la función derivada de una función. Las reglas de derivación nos permiten calcular dericvadas sin calcular límites.
- 22 ejemplos sencillos de aplicación de las reglas de derivación.
Regla de la cadena
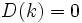
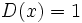
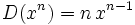
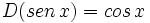
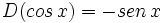
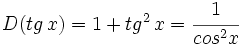
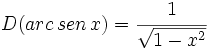
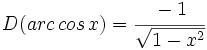
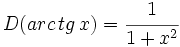
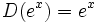
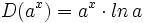
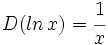
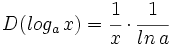
![D[k\,f(x)]=k\,f'(x)\;](/wikipedia/images/math/1/e/1/1e1df26b1290307dd9f35c29b3314606.png)
![D[f(x)+g(x)]=f'(x)+g'(x)\;](/wikipedia/images/math/5/d/7/5d79cbe9e2246a5e1ec6da9fbc79488a.png)
![D[f(x) \cdot g(x)]=f'(x) \cdot g(x) + f(x) \cdot g'(x)\;](/wikipedia/images/math/f/f/2/ff213fdc8e847b6f0297c2bfe5bc7bc9.png)
![D[\cfrac{f(x)}{g(x)}]=\cfrac{f'(x) \cdot g(x) + f(x) \cdot g'(x)}{g(x)^2}\;](/wikipedia/images/math/f/e/4/fe45da01c411b12625beba843e230b4e.png)
![D{g[f(x)]}=g'[f(x)] \cdot f'(x)\;](/wikipedia/images/math/3/6/c/36cf5be8bad7b25cc694c247f0ab491a.png)

