Plantilla:Def m.c.m.

(Diferencia entre revisiones)

Revisión de 18:05 3 may 2017

El mínimo común múltiplo (m.c.m.) de dos o más números, es el menor de todos los múltiplos comunes a esos números.

Cálculo del mínimo común múltiplo

Para obtener el m.c.m. de dos o más números, se descomponen los números en factores primos y se toman todos los factores elevados al mayor exponente.

Ejemplo:

Calcula el m.c.m.(24,60):

Primer método:

Múltiplos de 24: 24, 48, 72, 96, 120, 144,...

Múltiplos de 60: 60, 120, 180, ...

m.c.m.(24,60)= 120

Segundo método:

Descomponemos 24 y 60 en sus factores primos:

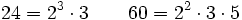
$24=2^3 \cdot 3\qquad60=2^2 \cdot 3 \cdot 5$

Multiplicando todos los factores elevados al mayor exponente:

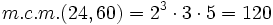
$m.c.m.(24,60)= 2^3 \cdot 3 \cdot 5=120$

{{p}ç

Ejemplos (12'12") Sinopsis:

Concepto de mínimo común múltiplo. Ejemplos.

 <center><math>m.c.m.(24,60)= 2^3 \cdot 3 \cdot 5=120</math></center>
 }}
+{{p}ç
+{{Video_enlace_julioprofe
+|titulo1=Ejemplos
+|duracion=12'12"
+|sinopsis=Concepto de mínimo común múltiplo. Ejemplos.
+|url1=https://www.youtube.com/watch?v=kxDeTxbnk-c
+}}
+{{p}}