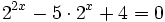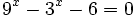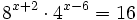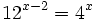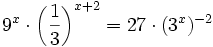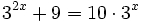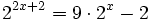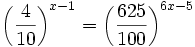Plantilla:Ecuaciones exponenciales
De Wikipedia
| Revisión de 09:06 4 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 09:23 4 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 135: | Línea 135: | ||
| |sinopsis=Resuelve: | |sinopsis=Resuelve: | ||
| - | :1. <math>4^{2x-5}=64\;</math> | + | :a) <math>4^{2x-5}=64\;</math> |
| - | :2. <math>7^{3-x}=5^{x+1}\;</math> | + | :b) <math>7^{3-x}=5^{x+1}\;</math> |
| |url1=https://www.youtube.com/watch?v=Fl1PvjOh9Us | |url1=https://www.youtube.com/watch?v=Fl1PvjOh9Us | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplo 3 | ||
| + | |duracion=5'01" | ||
| + | |sinopsis=Resuelve: | ||
| + | |||
| + | :<math>8^{x+2} \cdot 4^{x-6} =16\;</math> | ||
| + | |||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=_aZ10GXvUuM | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplo 4 | ||
| + | |duracion=7'29" | ||
| + | |sinopsis=Resuelve: | ||
| + | |||
| + | :<math>12^{x-2} = 4^x\;</math> | ||
| + | |||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=6ys1c3DIVNA | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplo 5 | ||
| + | |duracion=6'39" | ||
| + | |sinopsis=Resuelve: | ||
| + | |||
| + | :<math>9^x \cdot \left( \frac{1}{3} \right) ^{x+2} = 27 \cdot (3^x)^{-2}\;</math> | ||
| + | |||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=nR3INhQWHGc | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplo 6 | ||
| + | |duracion=6'23" | ||
| + | |sinopsis=Resuelve: | ||
| + | |||
| + | :<math>3^{2x} + 9=10\cdot 3^x\;</math> | ||
| + | |||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=CWfsbtVx24Q | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplo 7 | ||
| + | |duracion=10'27" | ||
| + | |sinopsis=Resuelve: | ||
| + | |||
| + | :<math>2^{2x+2} = 9 \cdot 2^x -2\;</math> | ||
| + | |||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=qA9Iggk09jQ | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplo 8 | ||
| + | |duracion=8'47" | ||
| + | |sinopsis=Resuelve: | ||
| + | |||
| + | :<math>\left( \frac{4}{10} \right) ^{x-1} = \left( \frac{625}{100} \right) ^{6x-5}\;</math> | ||
| + | |||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=iDKX--wp2U4 | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 09:23 4 may 2017
Las ecuaciones exponenciales son aquellas en las que la incógnita aparece como exponente.
Para su resolución hay que tener en cuenta las propiedades de las potencias y también puede ser necesario usar logaritmos.
Ejercicios resueltos: Ecuaciones exponenciales
Resuelve las siguientes ecuaciónes:
- a)
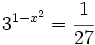
- b)
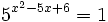
- c)
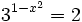
- d)
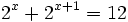
a)
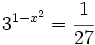
Expresamos el segundo miembro como potencia de 2:
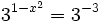
Como 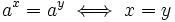 , los exponentes deben ser iguales:
, los exponentes deben ser iguales:
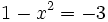
Y resolvemos la ecuación de segundo grado incompleta:
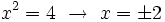
Soluciones: 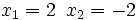
b)
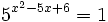
Expresamos el segundo miembro como potencia de 5:
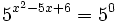
Como 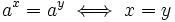 , los exponentes deben ser iguales:
, los exponentes deben ser iguales:
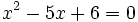
Resolvemos la ecuación de segundo grado:
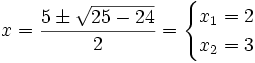
Soluciones: 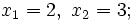
c)
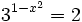
Como el segundo miembro no podemos expresarlo como potencia de base 3, tomaremos logaritmos en ambos lados de la ecuación:
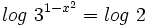
Aplicando la propiedad del logaritmo de una potencia:
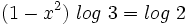
Y resolvemos la ecuación de segundo grado incompleta:
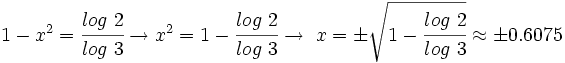
Soluciones: 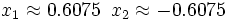
d)
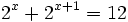
Haciendo el cambio de variable:
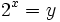
tenemos que:
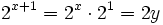
Y la ecuación de partida queda:

Resolvemos la ecuación de primer grado:
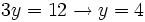
Y deshacemos el cambio de variable:
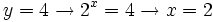
- Solución:
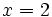
|
Actividad: Ecuaciones exponenciales Resuelve las siguientes ecuaciones:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ejemplos: Ecuaciones exponenciales
Resuelve:
- a)
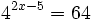
- b)
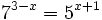
Resuelve:
Resuelve:
Resuelve:
Resuelve:
Resuelve:
Resuelve:
{{{sol}}}
![3^x=\sqrt[3]{9} \;](/wikipedia/images/math/d/b/0/db0233292d84043ca9d4101f6ac692a6.png)