Plantilla:Radicales (ampliación)
De Wikipedia
| Revisión de 17:13 17 may 2017 Coordinador (Discusión | contribuciones) (→Introducción de factores) ← Ir a diferencia anterior |
Revisión de 17:19 17 may 2017 Coordinador (Discusión | contribuciones) (→Introducción de factores) Ir a siguiente diferencia → |
||
| Línea 80: | Línea 80: | ||
| |sinopsis=Introduce los factores dentro del radical: <math>m^2n^5 \sqrt[5]{m^3 p^2}</math> | |sinopsis=Introduce los factores dentro del radical: <math>m^2n^5 \sqrt[5]{m^3 p^2}</math> | ||
| + | Para introducir un factor dentro de un radical, éste se eleva al índice del radical y el resultado se multiplica por el radicando del radical. De esta manera, para introducir una potencia dentro de un radical multiplicaremos el exponente de la potencia por el índice del radical y le sumaremos el exponente de la potencia con la misma base que haya dentro del radical. | ||
| |url1=https://www.youtube.com/watch?v=rEljk_OzcY0 | |url1=https://www.youtube.com/watch?v=rEljk_OzcY0 | ||
| }} | }} | ||
Revisión de 17:19 17 may 2017
Tabla de contenidos |
Extracción e introducción de factores en un radical
Extracción de factores
Para extaer factores de un radical se divide el exponente entre el índice y se saca el factor elevado al cociente de la división quedando ese factor elevado al resto.
Ejemplo: Extracción de factores de un radical
Extrae todo lo que se pueda de este radical: ![\sqrt[3]{6000}](/wikipedia/images/math/5/c/2/5c28fba2f76ed7b33ea1b13e448c224f.png)
![\sqrt[3]{6000}=\sqrt[3]{2^4 \cdot 3 \cdot 5^3}=2 \cdot 5 \sqrt[3]{2 \cdot 3}=10\sqrt[3]{6}](/wikipedia/images/math/6/9/f/69fad43d23404b125d2e89b1f9479c74.png)
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Simplifica: ![-2\sqrt [3]{16x^5yz^9}](/wikipedia/images/math/5/d/a/5da6c4122805a4279103f0cf5cfb13c0.png)
Simplifica: ![\sqrt [4]{32x^4y^{21}z^{43}}](/wikipedia/images/math/c/4/f/c4f4294a30ee9a53a181d8f3abd8d54b.png)
Simplifica: ![\sqrt [5]{32x^5y^{-10}z^{-35}}](/wikipedia/images/math/e/f/b/efb9fab775fddc918c97f70c90e23eb4.png)
Simplifica: ![\sqrt [5]{-243a^{20}}](/wikipedia/images/math/e/e/3/ee38623c8fe3fac34be9faf93f9e8457.png)
Introducción de factores
Para introducir un factor dentro de un radical, éste se eleva al índice del radical y el resultado se multiplica por el radicando del radical.
Ejemplo: Introducción de factores en un radical
Introduce los factores dentro del radical: ![10 \sqrt[3]{6}](/wikipedia/images/math/b/0/5/b059e301f3cf30968be2c858922be777.png)
![10 \sqrt[3]{6}=\sqrt[3]{6 \cdot 10^3}=\sqrt[3]{6000}](/wikipedia/images/math/f/c/a/fca24b7a66a69b8d0a52ef1d1f43ef96.png)
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Introduce los factores dentro del radical: ![m^2n^5 \sqrt[5]{m^3 p^2}](/wikipedia/images/math/2/7/6/276aa6fd087cafe6e44377e54dfae158.png)
Para introducir un factor dentro de un radical, éste se eleva al índice del radical y el resultado se multiplica por el radicando del radical. De esta manera, para introducir una potencia dentro de un radical multiplicaremos el exponente de la potencia por el índice del radical y le sumaremos el exponente de la potencia con la misma base que haya dentro del radical.
Pulsa el botón EJERCICIO y verás el enunciado; hazlo en tu cuaderno e introduce la solución con la escena, luego pulsa el botón SOLUCIÓN para ver si lo has hecho bien.
Simplifica:
- a)
![\sqrt[3]{5^{17} \cdot 4^6}](/wikipedia/images/math/0/0/5/005d7f0a77ef68096dbc57b6faf62174.png)
- b)
![\sqrt[3]{16\, a^4\, b^{21}}](/wikipedia/images/math/1/0/a/10a9ce8e21e1692804f04887051c25a2.png)
- c)
![7^3 \cdot 6^9 \sqrt[11]{y^3}](/wikipedia/images/math/6/d/d/6dd037766dcba2853e802af0eb172662.png)
Suma y resta de radicales con el mismo índice y distinto radicando
Si tienen el mismo índice pero distinto radicando, a veces, podemos extraer factores del radical y dejarlos con el mismo radicando.
Ejemplo: Suma y resta de radicales con el mismo índice y distinto radicando
Resta los siguientes radicales: 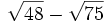

Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Simplifica: 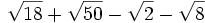
Simplifica: 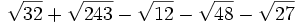
Pulsa el botón EJERCICIO y verás el enunciado; hazlo en tu cuaderno e introduce la solución con la escena, luego pulsa el botón SOLUCIÓN para ver si lo has hecho bien.
En esta escena podrás practicar la suma y resta de radicales con o sin el mismo índice.
Producto y cocientes de radicales de distinto índice
Para multiplicar o dividir radicales de distinto índice, primero se reducen a índice común y luego se multiplican o dividen los radicandos.
Ejemplo: Producto y cocientes de radicales de distinto índice
Reduce a un solo radical ![\sqrt[3]{10} \cdot \sqrt[4]{5}:\sqrt{8}](/wikipedia/images/math/5/9/7/597ebbc8a8a1e63faeabbecf3da740ef.png)
Para reducir los radicales a índice común calculamos el m.c.m de los índices: m.c.m.(3,4,2)=12 y elevamos cada radicando al resultado de dividir el m.c.m. por el índice de cada radical.
![\sqrt[3]{10} \cdot \sqrt[4]{5}:\sqrt{8}=\sqrt[12]{10^4} \cdot \sqrt[12]{5^3}:\sqrt[12]{8^6}](/wikipedia/images/math/e/8/1/e81ffde8d1c752d66e97b66e25149a0f.png)
Luego multiplicamos o dividimos los radicandos, ya que ahora los índices son iguales:
![\sqrt[12]{10^4} \cdot \sqrt[12]{5^3}:\sqrt[12]{8^6}=\sqrt[12]{10^4 \cdot 5^3 : 8^6}](/wikipedia/images/math/6/d/1/6d1f82fd6b85971e0e493c1e7eb2d485.png)
Finalmente simplificamos:
![\sqrt[12]{10^4 \cdot 5^3 : 8^6}=\sqrt[12]{2^4 \cdot 5^4 \cdot 5^3 : (2^3)^6}=\sqrt[12]{2^{-14} \cdot 5^7}](/wikipedia/images/math/7/0/e/70e1e7afd0d65ac459a2b76336b7fbb6.png)
Simplifica: ![(8\sqrt[3]{a^2b}) \cdot (4\sqrt{ab^3})](/wikipedia/images/math/8/e/a/8ea372bbacf499b888b5f31aeb1cae8b.png)
Simplifica: ![\sqrt[3]{27^{-2}} : \sqrt[4]{16}](/wikipedia/images/math/1/0/d/10dcb2912a1fddcdb4f0013df23cedc3.png)
Actividades
Simplifica:
a)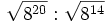
b)![\sqrt[6]{\sqrt{8}}](/wikipedia/images/math/b/d/b/bdbeee310b4a724e942f08bffbfa8d23.png)
c)![\sqrt[9]{12} \cdot \sqrt{3}](/wikipedia/images/math/7/2/8/72833303cca23937986fcffc7c483ab7.png)
Simplifica: 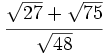
Simplifica: ![\sqrt [4]{\sqrt{x^3} \cdot 16 \sqrt{x}}](/wikipedia/images/math/c/b/1/cb16004d071779fc6b1ffc6f93945a68.png)
Simplifica: ![\left(\cfrac{\sqrt [6]{32}}{\sqrt{8}} \right)^3](/wikipedia/images/math/e/a/c/eacfafeb055cc8c9cdb0aad1d2009d5a.png)
![\sqrt[4]{3} - \sqrt[4]{243}](/wikipedia/images/math/e/6/6/e66fc6d8653c96dff0e3c0b95dc93b55.png)

