Plantilla:Radicales (ampliación)
De Wikipedia
| Revisión de 07:45 22 may 2017 Coordinador (Discusión | contribuciones) (→Extracción de factores) ← Ir a diferencia anterior |
Revisión de 07:49 22 may 2017 Coordinador (Discusión | contribuciones) (→Extracción de factores) Ir a siguiente diferencia → |
||
| Línea 41: | Línea 41: | ||
| {{p}} | {{p}} | ||
| {{Videotutoriales|titulo=Extracción de factores de un radical|enunciado= | {{Videotutoriales|titulo=Extracción de factores de un radical|enunciado= | ||
| - | {{Video_enlace_julioprofe | + | {{Video_enlace_abel |
| |titulo1=Ejemplo 1 | |titulo1=Ejemplo 1 | ||
| - | |duracion=3'40" | + | |duracion=26'16" |
| |sinopsis=Simplifica: <math>-2\sqrt [3]{16x^5yz^9}</math> | |sinopsis=Simplifica: <math>-2\sqrt [3]{16x^5yz^9}</math> | ||
| |url1=https://www.youtube.com/watch?v=yQmn2rmM_t8&list=PL9B9AC3136D2D4C45&index=78 | |url1=https://www.youtube.com/watch?v=yQmn2rmM_t8&list=PL9B9AC3136D2D4C45&index=78 | ||
| }} | }} | ||
| - | {{p}} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| |titulo1=Ejemplo 2 | |titulo1=Ejemplo 2 | ||
| + | |duracion=3'40" | ||
| + | |sinopsis=Extrae fuera del radical: | ||
| + | |||
| + | a) <math>\sqrt{72}\;</math>{{b4}}{{b4}}b) <math>\sqrt[4]{3645}\;</math>{{b4}}{{b4}}c) <math>\sqrt{3240}\;</math>{{b4}}{{b4}}c) <math>5\,\sqrt[3]{384}\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=Rz-wClV7awM | ||
| + | }} | ||
| + | |||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplo 3 | ||
| |duracion=4'12" | |duracion=4'12" | ||
| |sinopsis=Simplifica: <math>\sqrt [4]{32x^4y^{21}z^{43}}</math> | |sinopsis=Simplifica: <math>\sqrt [4]{32x^4y^{21}z^{43}}</math> | ||
| Línea 57: | Línea 67: | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejemplo 3 | + | |titulo1=Ejemplo 4 |
| |duracion=2'54" | |duracion=2'54" | ||
| |sinopsis=Simplifica: <math>\sqrt [5]{32x^5y^{-10}z^{-35}}</math> | |sinopsis=Simplifica: <math>\sqrt [5]{32x^5y^{-10}z^{-35}}</math> | ||
| Línea 63: | Línea 73: | ||
| {{p}} | {{p}} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejemplo 4 | + | |titulo1=Ejemplo 5 |
| |duracion=2'03" | |duracion=2'03" | ||
| |sinopsis=Simplifica: <math>\sqrt [5]{-243a^{20}}</math> | |sinopsis=Simplifica: <math>\sqrt [5]{-243a^{20}}</math> | ||
Revisión de 07:49 22 may 2017
Tabla de contenidos |
Extracción e introducción de factores en un radical
Extracción de factores
Procedimiento
Para extraer factores de un radical se divide el exponente (m) del factor entre el índice (n) del radical. A continuación, se saca el factor elevado al cociente (c) de la división, quedando dentro del radical el factor elevado al resto (r).
![\sqrt[n]{a^m}= a^c \cdot \sqrt[n]{a^r}](/wikipedia/images/math/5/e/c/5ecb8e4f6515ae774c6eef7fea5c576e.png)
Para la demostración transformaremos la expresión radical en potencias y aplicaremos las propiedades de las operaciones con potencias:
Fíjate que en (1) hemos usado la regla de la divsión:
Para extraer factores de un radical se divide el exponente entre el índice y se saca el factor elevado al cociente de la división quedando ese factor elevado al resto.
Ejemplo: Extracción de factores de un radical
Extrae todo lo que se pueda de este radical: ![\sqrt[3]{6000}](/wikipedia/images/math/5/c/2/5c28fba2f76ed7b33ea1b13e448c224f.png)
![\sqrt[3]{6000}=\sqrt[3]{2^4 \cdot 3 \cdot 5^3}=2 \cdot 5 \sqrt[3]{2 \cdot 3}=10\sqrt[3]{6}](/wikipedia/images/math/6/9/f/69fad43d23404b125d2e89b1f9479c74.png)
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Introducción de factores
Procedimiento
Para introducir un factor dentro de un radical, éste se eleva al índice del radical y el resultado se multiplica por el radicando del radical.
![a \sqrt[n]{b}= \sqrt[n]{a^n \cdot b}](/wikipedia/images/math/8/5/f/85f82704cfc0f9e1418d853a9e18061d.png)
Para la demostración transformaremos la expresión radical en potencias y aplicaremos las propiedades de las operaciones con potencias:
Ejemplo: Introducción de factores en un radical
Introduce los factores dentro del radical: ![10 \sqrt[3]{6}](/wikipedia/images/math/b/0/5/b059e301f3cf30968be2c858922be777.png)
![10 \sqrt[3]{6}=\sqrt[3]{6 \cdot 10^3}=\sqrt[3]{6000}](/wikipedia/images/math/f/c/a/fca24b7a66a69b8d0a52ef1d1f43ef96.png)
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Introduce dentro del radical: 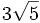
Para introducir un factor dentro de un radical, éste se eleva al índice del radical y el resultado se multiplica por el radicando del radical. De esta manera, y teniendo en cuenta las propiedades de las operaciones con potencias, para introducir una potencia dentro de un radical multiplicaremos el exponente de la potencia por el índice del radical. La potencia resultante pasará dentro del radical multiplicando al radicando.
Introduce los factores dentro del radical: ![a^3 b^2 \sqrt[4]{c}](/wikipedia/images/math/0/f/2/0f257d67a28e35c2fe66d6e47ec6170b.png)
Para introducir un factor dentro de un radical, éste se eleva al índice del radical y el resultado se multiplica por el radicando del radical. De esta manera, y teniendo en cuenta las propiedades de las operaciones con potencias, para introducir una potencia dentro de un radical multiplicaremos el exponente de la potencia por el índice del radical. La potencia resultante pasará dentro del radical multiplicando al radicando.
Introduce los factores dentro del radical: ![m^2 n^5 \sqrt[5]{m^3 p^2}](/wikipedia/images/math/2/7/6/276aa6fd087cafe6e44377e54dfae158.png)
Para introducir un factor dentro de un radical, éste se eleva al índice del radical y el resultado se multiplica por el radicando del radical. De esta manera, y teniendo en cuenta las propiedades de las operaciones con potencias, para introducir una potencia dentro de un radical multiplicaremos el exponente de la potencia por el índice del radical. La potencia resultante pasará dentro del radical multiplicando al radicando. Si dentro del radical tenemos otra potencia con la misma base entonces sumaremos el exponente de la potencia que entra con el de dentro del radical.
Pulsa el botón EJERCICIO y verás el enunciado; hazlo en tu cuaderno e introduce la solución con la escena, luego pulsa el botón SOLUCIÓN para ver si lo has hecho bien.
Suma y resta de radicales con el mismo índice y distinto radicando
Si tienen el mismo índice pero distinto radicando, a veces, podemos extraer factores del radical y dejarlos con el mismo radicando.
Ejemplo: Suma y resta de radicales con el mismo índice y distinto radicando
Resta los siguientes radicales: 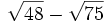

Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Pulsa el botón EJERCICIO y verás el enunciado; hazlo en tu cuaderno e introduce la solución con la escena, luego pulsa el botón SOLUCIÓN para ver si lo has hecho bien.
En esta escena podrás practicar la suma y resta de radicales con o sin el mismo índice.
Producto y cocientes de radicales con distinto índice
Para multiplicar o dividir radicales con distinto índice, primero se reducen a índice común y luego se multiplican o dividen los radicandos.
Ejemplo: Producto y cocientes de radicales con distinto índice
Reduce a un solo radical ![\sqrt[3]{10} \cdot \sqrt[4]{5}:\sqrt{8}](/wikipedia/images/math/5/9/7/597ebbc8a8a1e63faeabbecf3da740ef.png)
Para reducir los radicales a índice común calculamos el m.c.m de los índices: m.c.m.(3,4,2)=12 y elevamos cada radicando al resultado de dividir el m.c.m. por el índice de cada radical.
![\sqrt[3]{10} \cdot \sqrt[4]{5}:\sqrt{8}=\sqrt[12]{10^4} \cdot \sqrt[12]{5^3}:\sqrt[12]{8^6}](/wikipedia/images/math/e/8/1/e81ffde8d1c752d66e97b66e25149a0f.png)
Luego multiplicamos o dividimos los radicandos, ya que ahora los índices son iguales:
![\sqrt[12]{10^4} \cdot \sqrt[12]{5^3}:\sqrt[12]{8^6}=\sqrt[12]{10^4 \cdot 5^3 : 8^6}](/wikipedia/images/math/6/d/1/6d1f82fd6b85971e0e493c1e7eb2d485.png)
Finalmente simplificamos:
![\sqrt[12]{10^4 \cdot 5^3 : 8^6}=\sqrt[12]{2^4 \cdot 5^4 \cdot 5^3 : (2^3)^6}=\sqrt[12]{2^{-14} \cdot 5^7}](/wikipedia/images/math/7/0/e/70e1e7afd0d65ac459a2b76336b7fbb6.png)
Actividades
Simplifica:
a)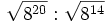
b)![\sqrt[6]{\sqrt{8}}](/wikipedia/images/math/b/d/b/bdbeee310b4a724e942f08bffbfa8d23.png)
c)![\sqrt[9]{12} \cdot \sqrt{3}](/wikipedia/images/math/7/2/8/72833303cca23937986fcffc7c483ab7.png)
Simplifica: 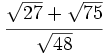
Simplifica: ![\sqrt [4]{\sqrt{x^3} \cdot 16 \sqrt{x}}](/wikipedia/images/math/c/b/1/cb16004d071779fc6b1ffc6f93945a68.png)
Simplifica: ![\left(\cfrac{\sqrt [6]{32}}{\sqrt{8}} \right)^3](/wikipedia/images/math/e/a/c/eacfafeb055cc8c9cdb0aad1d2009d5a.png)
Simplifica (Extracción e introducción de factores en un radical):
- a)
![\sqrt[3]{5^{17} \cdot 4^6}](/wikipedia/images/math/0/0/5/005d7f0a77ef68096dbc57b6faf62174.png)
- b)
![\sqrt[3]{16\, a^4\, b^{21}}](/wikipedia/images/math/1/0/a/10a9ce8e21e1692804f04887051c25a2.png)
- c)
![7^3 \cdot 6^9 \sqrt[11]{y^3}](/wikipedia/images/math/6/d/d/6dd037766dcba2853e802af0eb172662.png)
![\sqrt[n]{a^m}= a^{\frac{m}{n}} \begin{matrix} ~_{(1)}~ \\ = \\ \, \end{matrix} a^{c+\frac{r}{n}}= a^c \cdot a^{\frac{r}{n}}= a^c \cdot \sqrt[n]{a^r}](/wikipedia/images/math/d/3/9/d39083130ff7fc81f2df907b77c139e4.png)
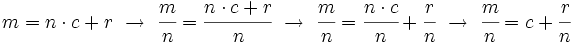
![-2\sqrt [3]{16x^5yz^9}](/wikipedia/images/math/5/d/a/5da6c4122805a4279103f0cf5cfb13c0.png)
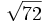 b)
b) ![\sqrt[4]{3645}\;](/wikipedia/images/math/6/4/e/64e81b0470d1d706dc6259ee3c15b821.png) c)
c) 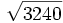 c)
c) ![5\,\sqrt[3]{384}\;](/wikipedia/images/math/4/9/0/4905ec017f8b5e0d98f7ee1f7eec1207.png)
![\sqrt [4]{32x^4y^{21}z^{43}}](/wikipedia/images/math/c/4/f/c4f4294a30ee9a53a181d8f3abd8d54b.png)
![\sqrt [5]{32x^5y^{-10}z^{-35}}](/wikipedia/images/math/e/f/b/efb9fab775fddc918c97f70c90e23eb4.png)
![\sqrt [5]{-243a^{20}}](/wikipedia/images/math/e/e/3/ee38623c8fe3fac34be9faf93f9e8457.png)
![a \sqrt[n]{b}=a \cdot b^{\frac{1}{n}}=(a^n)^{\frac{1}{n}} \cdot b^{\frac{1}{n}}= (a^n \cdot b)^{\frac{1}{n}}= \sqrt[n]{a^n \cdot b}](/wikipedia/images/math/7/9/3/793321a371ba1c1c188fd5e877399640.png)
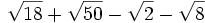
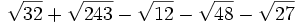
![\sqrt[4]{3} - \sqrt[4]{243}](/wikipedia/images/math/e/6/6/e66fc6d8653c96dff0e3c0b95dc93b55.png)
![(8\sqrt[3]{a^2b}) \cdot (4\sqrt{ab^3})](/wikipedia/images/math/8/e/a/8ea372bbacf499b888b5f31aeb1cae8b.png)
![\sqrt[3]{27^{-2}} : \sqrt[4]{16}](/wikipedia/images/math/1/0/d/10dcb2912a1fddcdb4f0013df23cedc3.png)

