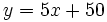Expresión analítica de una función (3ºESO Académicas)
De Wikipedia
| Revisión de 17:23 5 nov 2016 Coordinador (Discusión | contribuciones) (→Expresión analítica de una función) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Variables discretas y continuas) |
||
| Línea 9: | Línea 9: | ||
| (Pág. 152) | (Pág. 152) | ||
| ==Expresión analítica de una función== | ==Expresión analítica de una función== | ||
| + | {{Expresión analítica de una función}} | ||
| + | {{p}} | ||
| {{Wolfram: Tabla de valores de una función}} | {{Wolfram: Tabla de valores de una función}} | ||
| + | {{p}} | ||
| + | |||
| + | ==Dominio de una función dada por una expresión analítica== | ||
| + | {{Determinación del dominio de una función}} | ||
| {{p}} | {{p}} | ||
| {{Wolfram: Dominio e imagen}} | {{Wolfram: Dominio e imagen}} | ||
| {{p}} | {{p}} | ||
| - | ===Determinación del dominio de una función=== | + | |
| - | {{Determinación del dominio de una función}} | + | |
| + | |||
| + | ==Ejercicios== | ||
| + | {{ejercicio: variables discrestas y continuas}} | ||
| {{p}} | {{p}} | ||
| ===Ejercicios propuestos=== | ===Ejercicios propuestos=== | ||
Revisión actual
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 152)
Expresión analítica de una función
La expresión analítica de una función es una ecuación que relaciona la variable dependiente con la variable independiente.
Ejemplo: Expresión analítica de una función
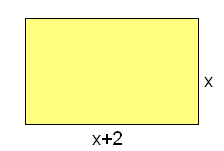
Un rectángulo mide 2 cm más de largo que de ancho.
- Halla la expresión analítica de la función que relaciona su área con su lado menor. Halla su dominio.
- Halla la expresión analítica de la función que relaciona su perímetro con su lado menor. Halla su dominio.
- Haz una tabla de valores para cada función.
- Representa gráficamente las dos funciones anteriores.
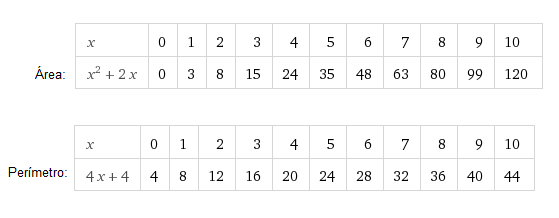
3. Tablas de valores:
4. Representación gráfica: A partir de los valores de las tablas anteriores, dibujamos los puntos de las gráficas: la dell área (en verde) y la del perímetro (en marrón).
Tutorial en el que se explican los conceptos básicos de la función y de su expresión analítica (expresión en forma de fórmula): variable independiente, dependiente, imagen, preimagen, dominio, recorrido...
Representación gráfica de funciones básicas
Se va a construir una caja rectangular sin tapa a partir de una lámina metálica de 30 cm de largo por 20 cm de ancho. Para ello se van a recortar cuadrados de lado "x" en las esquinas y luego se van a doblar los lados hacia arriba. Obtén la expresión analítica que relaciona el volumen "V" de la caja en función del lado "x".
Expresa el área "A" de un triángulo equilátero en función de sus lado "L".
Dada la ecuación 4a + 7b = -52, encuentra la expresión analítica de la función a = f(b) que relacione la variable independiente b con la variable dependiente a, es decir, que exprese a en función de b.
Tutorial en el que se trabaja con las funciones definidas por partes en fórmulas, cálculo de imágenes y preimágenes de valores.
Actividades con las que aprenderás a obtener la expresión analítica de una función descrita mediante un enunciado.
Escribir funciones a partir de ecuaciones.
|
Actividad: Expresión analítica de una función Dadas las funciones
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Dominio de una función dada por una expresión analítica
El dominio de una función puede estar determinado o limitado por diferentes razones:
- Imposibilidad de realizar alguna operación con ciertos valores de
 (Por ejemplo, si en la expresión analítica aparecen denominadores que se anulan o radicandos que toman valores negativos)
(Por ejemplo, si en la expresión analítica aparecen denominadores que se anulan o radicandos que toman valores negativos)
- Contexto en el que se estudia la función (Por ejemplo, una función que relaciona lado y área de una figura plana, el lado no puede tomar valores negativos)
- Por voluntad de quien propone la función (A veces nos puede interesar estudiar sólo un trozo de la función).
Ejemplos: Dominio de una función dada por una expresión analítica
- Halla el dominio de las funciones:
- a)
![y=x-3 \ , \quad x \in [-1,1]\;\!](/wikipedia/images/math/b/2/f/b2f9332046e953e44d840dc3a97e95ea.png)
- a)
- b)
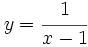
- b)
- c)
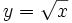
- c)
- d)
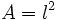 (Área de un cuadrado de lado
(Área de un cuadrado de lado 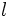 )
)
- d)
- a) Su dominio es
![[-1,1]\;\!](/wikipedia/images/math/d/e/f/defe3e8e42c39a844e648621afe1619e.png) , por voluntad del que ha definido la función, ya que, en principio, cualquier valor de
, por voluntad del que ha definido la función, ya que, en principio, cualquier valor de  da un valor de
da un valor de 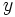 válido.
válido.
- b) Su dominio es
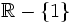 , porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
, porque el denominador no puede tomar el valor cero, ya que imposibilitaría hacer la división.
- c) Su dominio es
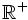 , porque el radicando no puede ser negativo para poder hallar la raíz.
, porque el radicando no puede ser negativo para poder hallar la raíz.
- d) Su dominio es
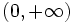 , porque el lado de un cuadrado sólo puede tomar valores positivos
, porque el lado de un cuadrado sólo puede tomar valores positivos
Intervalos. Notación.
Dominio de una función.
Rango o imagen de una función.
Conceptos de dominio y rango de una función. Ejemplos
Dominio y rango de una función. Ejemplos.
Halla el dominio de 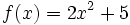 .
.
Halla el dominio de 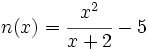 .
.
Halla el dominio de 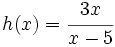 .
.
Halla el dominio de 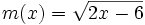 .
.
Halla el dominio de 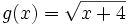 .
.
Halla el dominio de 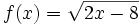 .
.
Dominio de una función dada por su expresión analítica.
|
Actividad: Dominio e imagen de una función
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ejercicios
|
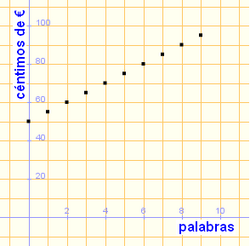
Ejercicio resuelto: Variables discretas y continuas Poner una anuncio por palabras cuesta una cantidad fija de 0.50 €, más 0.05 € por cada palabra.
|
Ejercicios propuestos
|
Ejercicios propuestos: Expresión analítica de una función |
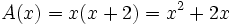
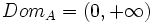
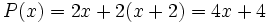
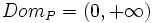
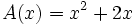
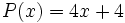
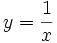 .
.