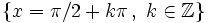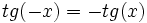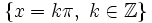Funciones trigonométricas o circulares (1ºBach)
De Wikipedia
| Revisión de 18:11 21 may 2017 Coordinador (Discusión | contribuciones) (→Función coseno) ← Ir a diferencia anterior |
Revisión de 16:47 10 jun 2017 Coordinador (Discusión | contribuciones) (→Función tangente) Ir a siguiente diferencia → |
||
| Línea 102: | Línea 102: | ||
| {{p}} | {{p}} | ||
| - | + | ==Actividades y videotutoriales== | |
| + | {{Video_enlace2 | ||
| + | |titulo1=Estudio de la periodicidad de las funciones trigonométricas | ||
| + | |duracion=14'00" | ||
| + | |url1=https://www.youtube.com/watch?v=5nEUzbQZtBs | ||
| + | |sinopsis=Estudio de la periodicidad de las funciones trigonométricas. | ||
| + | }} | ||
| {{wolfram desplegable|titulo=Funciones trigonométricas|contenido= | {{wolfram desplegable|titulo=Funciones trigonométricas|contenido= | ||
| {{wolfram | {{wolfram | ||
Revisión de 16:47 10 jun 2017
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Funciones trigonométricas
Vamos a estudiar las funciones que se obtienen a partir de las razones trigonométricas de un ángulo x al hacer variar éste. Dicho ángulo se suele expresar en radianes.
En esta escena podrás ver como se representan las funciones trigonométricas.
Estudio gráfico de las funciones seno y coseno.
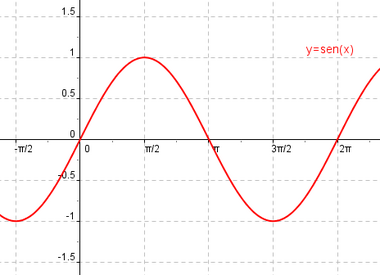
Función seno
Se define la función seno como 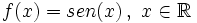 |
Definición, representación y análisis de la función seno.
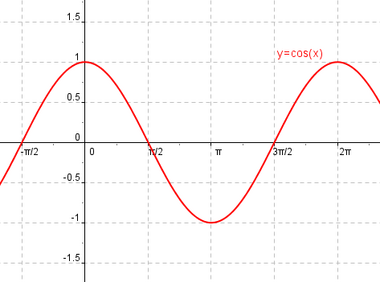
Función coseno
Se define la función coseno como 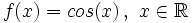 |
Definición, representación y análisis de la función coseno.
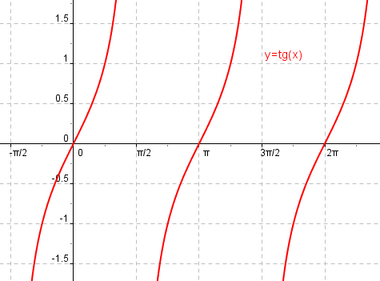
Función tangente
Se define la función coseno como 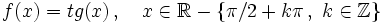 Propiedades de la función tangente
|
Actividades y videotutoriales
Estudio de la periodicidad de las funciones trigonométricas.
|
Actividad: Funciones trigonométricas
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
En esta escena podrás ver como se obtiene el ángulo conocida una razón, de forma gráfica, utilizando la representación gráfica de las funciones trigonométricas.
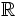
![[-1, 1]\,](/wikipedia/images/math/5/8/1/581a26dec23e9f937a02a278e20fc9c3.png)
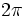 .
.
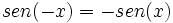
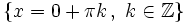
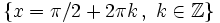
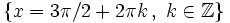
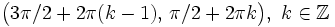 .
.
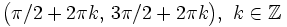 .
.
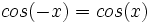
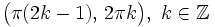 .
.
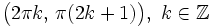 .
.
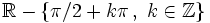
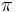 .
.