Regla de L´Hôpital (2ºBach)
De Wikipedia
| Revisión de 10:37 21 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 6: | Línea 6: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Video_enlace2 | + | {{Regla de LHopital}} |
| - | |titulo1=Regla de L´Hôpital | + | |
| - | |duracion=7'17" | + | |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0427.html | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{ejemplo2 | + | |
| - | |titulo=Ejemplos: ''Regla de L´Hôpital'' | + | |
| - | |enunciado= | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=1. Cociente de dos números que tienden a cero | + | |
| - | |duracion='" | + | |
| - | |sinopsis=:7 ejemplos | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0427_01.htm | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=2. Cociente de dos números que tienden a cero | + | |
| - | |duracion='" | + | |
| - | |sinopsis=:10 ejemplos | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0427_02.htm | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=3. Cociente de dos números que tienden a cero | + | |
| - | |duracion='" | + | |
| - | |sinopsis=:9 ejemplos | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0427_03.htm | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=4. Cociente de dos números que tienden a cero | + | |
| - | |duracion='" | + | |
| - | |sinopsis=:12 ejemplos | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0427_04.htm | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=5. Cociente de dos números que tienden a infinito | + | |
| - | |duracion='" | + | |
| - | |sinopsis= | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0427_05.htm | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=6. Tres avisos sobre la Regla de L'Hospital | + | |
| - | |duracion='" | + | |
| - | |sinopsis= | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0427_06.htm | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=7. Producto de un factor que tiende a cero por otro que tiende a infinito | + | |
| - | |duracion='" | + | |
| - | |sinopsis= | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0427_07.htm | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=8. Potencia con base que tiende a uno y exponente que tiende a infinito | + | |
| - | |duracion='" | + | |
| - | |sinopsis= | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0427_08.htm | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=9. Alternativa para potencia con base que tiende a uno y exponente que tiende a infinito | + | |
| - | |duracion='" | + | |
| - | |sinopsis= | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0427_09.htm | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=10. Potencia con base que tiende a cero con valores positivos y exponente que tiende a cero | + | |
| - | |duracion='" | + | |
| - | |sinopsis= | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0427_10.htm | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=11. Potencia con base que tiende a infinito y exponente que tiende a cero | + | |
| - | |duracion='" | + | |
| - | |sinopsis= | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0427_11.htm | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=12. Diferencia de dos números que tienden a infinito con igual signo | + | |
| - | |duracion='" | + | |
| - | |sinopsis= | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_04/vdf0427_12.htm | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{Videotutoriales|titulo=Límites trigonométricos|enunciado= | + | |
| - | {{Video_enlace_virtual | + | |
| - | |titulo1=Ejercicio 1 | + | |
| - | |duracion=6'09" | + | |
| - | |sinopsis=Calcula: <math>\lim_{x \to 0} \cfrac{tg \, 10x}{x}</math> | + | |
| - | |url1=https://www.youtube.com/watch?v=NS7l6ODc1Rg&index=1&list=PLo7_lpX1yruNjralkBxp5CTiYwieUtCI1 | ||
| - | }} | ||
| - | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 2 | ||
| - | |duracion=4'05" | ||
| - | |sinopsis=Calcula: <math>\lim_{t \to 0} \cfrac{sen^3 \, t}{(2t)^3}</math> | ||
| - | |||
| - | |url1=https://www.youtube.com/watch?v=M0fliU35wv8&list=PLo7_lpX1yruNjralkBxp5CTiYwieUtCI1&index=2 | ||
| - | }} | ||
| - | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 3 | ||
| - | |duracion=12'35" | ||
| - | |sinopsis=Calcula: <math>\lim_{x \to \frac{\pi}{2}} \cfrac{tg \, 2x}{x-\frac{\pi}{2}}</math> | ||
| - | |||
| - | |url1=https://www.youtube.com/watch?v=W_Dt4atA12g&list=PLo7_lpX1yruNjralkBxp5CTiYwieUtCI1&index=3 | ||
| - | }} | ||
| - | {{Video_enlace_virtual | ||
| - | |titulo1=Ejercicio 4 | ||
| - | |duracion=3'29" | ||
| - | |sinopsis=Calcula: <math>\lim_{x \to 0} \cfrac{sen \, 5x}{2x}</math> | ||
| - | |||
| - | |url1=https://www.youtube.com/watch?v=jNcwgWqf9nQ&list=PLo7_lpX1yruNjralkBxp5CTiYwieUtCI1&index=4 | ||
| - | }} | ||
| - | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Funciones]] | [[Categoría: Matemáticas]][[Categoría: Funciones]] | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Regla de L'Hôpital
Si al calcular 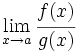 se presenta una indeterminación del tipo
se presenta una indeterminación del tipo 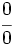 ó
ó 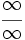 , y
, y 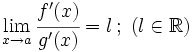 , entonces
, entonces 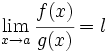 .
.
Esto también es cierto si 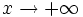 o
o 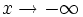 .
.
- Demostración de la regla de l'Hopital para el caso de indeterminación 0/0.
- Ejemplos de aplicación de la regla.
- Ejemplos en los que no se puede aplicar la regla por no verificarse las condiciones.
Ejercicio resuelto: Regla de L'Hôpital
Calcula:
- a)
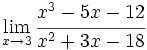
- b)

- c)
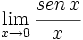
a) 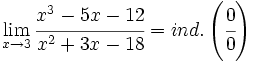
Aplicando la regla de L'Hôpital:
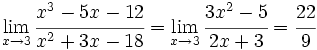
b) 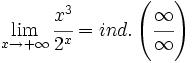
Aplicando la regla de L'Hôpital:
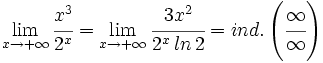
Aplicando la regla de L'Hôpital otra vez:
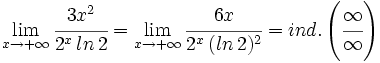
Y aplicando la regla de L'Hôpital una vez más:
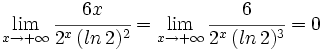
c)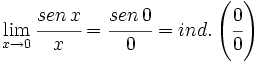
Aplicando la regla de L'Hôpital:
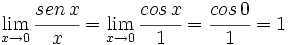
Regla de l'Hopital para los casos de indeterminación básicos. Ejemplos.
Regla de l'Hopital para todos los casos de indeterminación. Ejemplos.
Calcula: 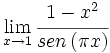
Calcula: 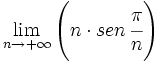
Calcula: 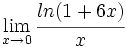
Calcula: 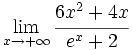
Calcula: 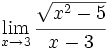
Calcula: 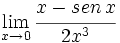
Calcula: 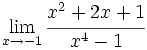
Regla de l'Hopital. Ejemplos en los que hay que aplicarla varias veces.
Calcula: 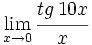
Calcula: 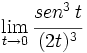
Calcula: 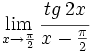
Calcula: 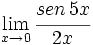
Calcula: 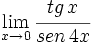
Calcula: 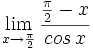
Calcula: 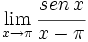
Calcula: 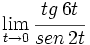
Calcula: 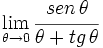
Calcula: 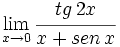
Calcula: 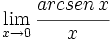
Calcula: