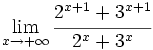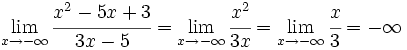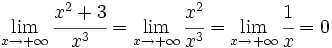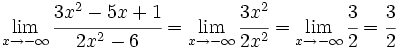Límites en el infinito (2ºBach)
De Wikipedia
| Revisión de 16:45 21 jun 2017 Coordinador (Discusión | contribuciones) (→Otros límites en el infinito) ← Ir a diferencia anterior |
Revisión de 16:46 21 jun 2017 Coordinador (Discusión | contribuciones) (→Límite en el infinito de funciones racionales) Ir a siguiente diferencia → |
||
| Línea 23: | Línea 23: | ||
| {{p}} | {{p}} | ||
| ==Límite en el infinito de funciones racionales== | ==Límite en el infinito de funciones racionales== | ||
| - | {{Video_enlace2 | + | {{Límite de funciones racionales cuando x tiende a infinito}} |
| - | |titulo1=Límite en el infinito de funciones racionales | + | |
| - | |duracion=6'22" | + | |
| - | |sinopsis= | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/02/di02_12.html | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{ejemplo2 | + | |
| - | |titulo=Ejemplos: ''Límite en el infinito de funciones racionales'' | + | |
| - | |enunciado= | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=1. Ejemplos | + | |
| - | |duracion=18'20" | + | |
| - | |sinopsis=6 ejemplos. | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/02/di02_12_01.html | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=2. Ejemplos | + | |
| - | |duracion=19'24" | + | |
| - | |sinopsis=6 ejemplos más. | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/02/di02_12_02.html | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=3. Ejemplos | + | |
| - | |duracion=8'14" | + | |
| - | |sinopsis=16 ejemplos. | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/02/di02_12_03.html | + | |
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| + | |||
| ==Otros límites en el infinito== | ==Otros límites en el infinito== | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
Revisión de 16:46 21 jun 2017
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
Límite en el infinito
Límite en el infinito de funciones polinómicas
Límite en el infinito de funciones racionales
Proposición
Consideremos la función racional en la variable x, ya simplificada:
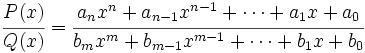
Se cumple que:
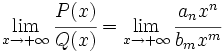 (análogamente si
(análogamente si  )
)Se pueden dar los siguientes casos:
- grado(P) > grado(Q): tras simplificar la fracción queda el límite de una función polinómica, que ya sabemos calcular, y que sabemos que puede ser
 ó
ó 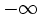 .
.
- grado(P ) = grado(Q): tras simplificar la fracción queda una constante,
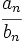 , que es el valor del límite.
, que es el valor del límite.
- grado(P) < grado(Q): tras simplificar la fracción queda una función inversa de una polinómica, cuyo límite sabemos que vale 0.
Límites cuando x tiende a infinito de cocientes de polinomios (método rápido) y diferencias de expresiones infinitas.
Límite de funciones racionales y de raíces de funciones racionales.
Caso 1: denominador con grado mayor que el numerador.
Caso 2: denominador con grado igual que el numerador.
Caso 3: denominador con grado menor que el numerador.
Para calcular el límite de un cociente de polinomios cuando x → +∞ o cuando x → -∞, dividimos numerador y denominador por la mayor potencia de "x" que aparezca en el denominador.
- Si numerador y denominador son de igual grado, el límite es el cociente de los coeficientes de los términos de mayor grado del numerador y el denominador.
- Si el numerador es de menor grado que el denominador, el límite es 0.
- Si el numerador es de mayor grado que el denominador, el límite es +∞ ó -∞ según que el numerador y el denominador tengan igual signo o no.
Calcula: 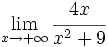
Calcula: 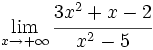
Calcula: 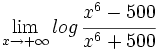
Límite de funciones racionales sencillas en el infinito.
Límite de funciones racionales en el infinito usando un método riguroso.
Límite de funciones racionales en el infinito usando un método riguroso.
Límite de funciones racionales en el infinito usando un método riguroso.
Límite de funciones racionales en el infinito usando un método riguroso.
Límite de funciones racionales en el infinito usando un método riguroso.
Límite de funciones racionales en el infinito usando un método riguroso.
Límite de funciones racionales en el infinito usando un método riguroso.
Otros límites en el infinito