Bisectriz de un ángulo (1º ESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:14 4 jul 2017 Coordinador (Discusión | contribuciones) (→Construcción de la bisectriz) ← Ir a diferencia anterior |
Revisión de 18:20 4 jul 2017 Coordinador (Discusión | contribuciones) (→Construcción de la bisectriz) Ir a siguiente diferencia → |
||
| Línea 22: | Línea 22: | ||
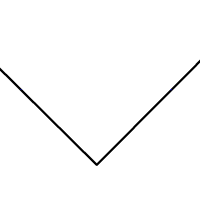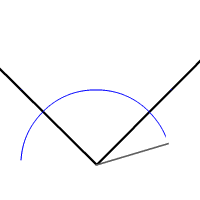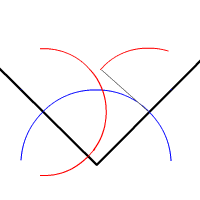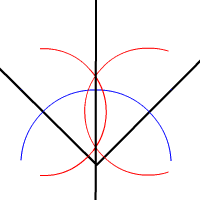
| {{Tabla75|celda2=[[Imagen:bisectriz_construct.gif|thumb|250px|Construcción de la bisectriz de un ángulo con regla y compás.]] | {{Tabla75|celda2=[[Imagen:bisectriz_construct.gif|thumb|250px|Construcción de la bisectriz de un ángulo con regla y compás.]] | ||
| |celda1= | |celda1= | ||
| - | Vamos a construir la mediatriz de un segmento utilizando regla y compás: | + | Vamos a construir la bisectriz de un ángulo utilizando regla y compás: |
| {{Teorema_sin_demo|titulo=Procedimiento|enunciado= | {{Teorema_sin_demo|titulo=Procedimiento|enunciado= | ||
| - | #Representa dos puntos y traza el segmento que los une utilizando la regla. | + | #Coloca el compás sobre el vértice, A, y traza un arco de circunferencia que corte a los dos lados, en los puntos, B y C. |
| - | #Coloca el compás sobre uno de los extremos del segmento y ábrelo para que coincida con el otro extremo. Traza así una circunferencia. Haz la misma operación apoyando el compás sobre el otro extremo y sin variar su abertura. | + | #Traza otros dos arcos, uno de centro B y radio BC y el segundo con centro C y radio BC. |
| - | #Une ahora los puntos donde se cortan las dos circunferencias que acabas de trazar. El nuevo segmento es perpendicular al inicial y si lo prolongas obtendrás la recta mediatriz que buscabas. | + | #Finalmente, une el vértice A con el punto donde se cortan los dos arcos que acabas de trazar y obtendrás la bisectriz del ángulo. |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Video_enlace_pdd|titulo1=Mediatriz de un segmento | + | {{Video_enlace_pdd|titulo1=Bisectriz de un ángulo |
| - | |duracion=2'09" | + | |duracion=2'14" |
| |url1=https://www.youtube.com/watch?v=1SKQFJDOi_Y | |url1=https://www.youtube.com/watch?v=1SKQFJDOi_Y | ||
| - | |sinopsis=En este vídeo trazamos la mediatriz de un segmento. | + | |sinopsis=En este vídeo trazamos la bisectriz de un ángulo por dos métodos. |
| }} | }} | ||
| {{p}} | {{p}} | ||
| {{AI_cidead | {{AI_cidead | ||
| - | |titulo1=Construcción de la mediatriz|descripcion=Actividad en la que podrás ver un video de cómo se construye la mediatriz de un segmento, utilizando regla y compás. También podrás hacerlo tú mismo con las herramientas de dibujo que se te proporcionan. | + | |titulo1=Construcción de la bisectriz|descripcion=Actividad en la que podrás ver un video de cómo se construye la bisectriz de un ángulo, utilizando regla y compás. También podrás hacerlo tú mismo con las herramientas de dibujo que se te proporcionan. |
| - | |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena8/1quincena8_contenidos_2b.htm | + | #Ejercicios resueltos. |
| + | |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena8/1quincena8_contenidos_4b.htm | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 18:20 4 jul 2017
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Bisectriz de un ángulo
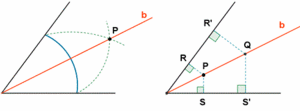
Se llama bisectriz de un ángulo a la semirrecta que, partiendo del vértice, lo divide en dos ángulos iguales.  Propiedad Los puntos de la bisectriz de un ángulo equidistan de los lados del mismo.  Bisectriz de un ángulo Descripción: Actividad en la que podrás ver la bisectriz de un ángulo y la propiedad de que sus puntos equidistan de los lados del ángulo. |  |
Construcción de la bisectriz
| Vamos a construir la bisectriz de un ángulo utilizando regla y compás:
Procedimiento
 Bisectriz de un ángulo (2'14") Sinopsis: En este vídeo trazamos la bisectriz de un ángulo por dos métodos. Construcción de la bisectriz Descripción: Actividad en la que podrás ver un video de cómo se construye la bisectriz de un ángulo, utilizando regla y compás. También podrás hacerlo tú mismo con las herramientas de dibujo que se te proporcionan.
 Construcción de la mediatriz Descripción: En esta escena podrás ver cómo se construye la mediatriz de un segmento, utilizando regla y compás. También podrás hacerlo tú mismo con las herramientas de dibujo que se te proporcionan. |  |
