Tendencias de una función (3ºESO Académicas)
De Wikipedia
| Revisión de 08:59 12 jul 2017 Coordinador (Discusión | contribuciones) (→Tendencia de una función) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Tendencia de una función) |
||
| Línea 19: | Línea 19: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Geogebra_enlace | + | {{AI: Tendencias}} |
| - | |descripcion=En esta escena podrás estudiar la tendencia de una función que relaciona la temperatura de un recipiente de agua que se va enfriando y el tiempo que ha transcurrido. | + | {{p}}{{p}} |
| - | |enlace=[https://ggbm.at/K3d3s2QB Tendencia de una función] | + | {{Ejercicios y videotutoriales: Tendencias}} |
| - | }} | + | |
| - | {{p}} | + | |
| - | + | ||
| - | {{p}} | + | |
| - | {{ejercicio | + | |
| - | |titulo=Ejercicio resuelto: ''Tendencia de una función'' | + | |
| - | |cuerpo= | + | |
| - | + | ||
| - | {{ejercicio_cuerpo | + | |
| - | |enunciado= | + | |
| - | '''1. '''Compramos un coche por 12.000 €, y cada año que pasa su precio se devalua un 20%. | + | |
| - | :a) Haz una tabla que exprese el precio del coche durante los próximos años. | + | |
| - | :b) Representa gráficamente los resultados del apartado a). | + | |
| - | :c) Encuentra una fórmula que exprese esta función. | + | |
| - | :d) ¿Cómo es la variable independiente: continua o discreta? | + | |
| - | :e) ¿Cuál es el dominio de esta función?. ¿Y su imagen? | + | |
| - | :f) ¿Cual es la tendencia de esta función segun pasan los años? | + | |
| - | :g) Describe el crecimiento e indica si tiene máximos o mínimos. | + | |
| - | + | ||
| - | {{p}} | + | |
| - | |sol= | + | |
| - | {{p}} | + | |
| - | :a) Tabla de valores:{{p}} | + | |
| - | <center> | + | |
| - | <table border="1" width="50%"> | + | |
| - | <tr> | + | |
| - | <td align="center" width="9%">{{b}}'''x'''{{b}}</td> | + | |
| - | <td align="center" width="9%">0</td> | + | |
| - | <td align="center" width="9%">1</td> | + | |
| - | <td align="center" width="9%">2</td> | + | |
| - | <td align="center" width="9%">3</td> | + | |
| - | <td align="center" width="9%">4</td> | + | |
| - | <td align="center" width="9%">5</td> | + | |
| - | <td align="center" width="9%">6</td> | + | |
| - | <td align="center" width="9%">7</td> | + | |
| - | </tr> | + | |
| - | <tr> | + | |
| - | <td align="center" width="9%">{{b}}'''y'''{{b}}</td> | + | |
| - | <td align="center" width="9%">12.000</td> | + | |
| - | <td align="center" width="9%">9.600</td> | + | |
| - | <td align="center" width="9%">7.680</td> | + | |
| - | <td align="center" width="9%">6.144</td> | + | |
| - | <td align="center" width="9%">4.915,2</td> | + | |
| - | <td align="center" width="9%">3.932,2</td> | + | |
| - | <td align="center" width="9%">3.145,7</td> | + | |
| - | <td align="center" width="9%">2.516,6</td> | + | |
| - | </tr> | + | |
| - | </table> | + | |
| - | </center> | + | |
| - | {{p}} | + | |
| - | :b) Representación gráfica: | + | |
| - | {{p}} | + | |
| - | [[Imagen:devalua.png|center|300px]]<br> | + | |
| - | :c) Continua. | + | |
| - | :d) <math>y=12\,000 \cdot 0.8^x \quad</math> (€) | + | |
| - | :e) <math>Dom_f=\mathbb{R}^+</math>; <math>Im_f=(0,12\,000]</math>. | + | |
| - | :f) La función tiende a 0 a medida que transcurre el tiempo. | + | |
| - | :g) Es decreciente en todo su dominio. Tiene un máximo en <math>x=0</math> y no tiene mínimos. | + | |
| - | + | ||
| - | }} | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{wolfram desplegable|titulo=Tendencias|contenido= | + | |
| - | {{wolfram | + | |
| - | |titulo=Actividad: ''Tendencias'' | + | |
| - | |cuerpo= | + | |
| - | {{ejercicio_cuerpo | + | |
| - | |enunciado= | + | |
| - | + | ||
| - | + | ||
| - | :a) Averigua la tendencia de la función <math>f(x)=\cfrac{1}{x}\;</math> cuando <math>x\;</math> se hace infinitamente grande. | + | |
| - | :b) Observa lo que ocurre en el apartado anterior dibujando la función desde x=0 a x=100000. | + | |
| - | + | ||
| - | {{p}} | + | |
| - | |sol= | + | |
| - | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | + | |
| - | + | ||
| - | :a) {{consulta|texto=limit x to +oo 1/x}} | + | |
| - | :b) {{consulta|texto=plot 1/x {x,0,100000}}} | + | |
| - | + | ||
| - | {{widget generico}} | + | |
| - | }} | + | |
| - | }} | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
Revisión actual
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 150)
Tendencia de una función
Decimos que una función 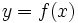 tiende a un valor
tiende a un valor 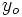 cuando aumenta la variable
cuando aumenta la variable  indefinidamente, si los valores de la variable dependiente
indefinidamente, si los valores de la variable dependiente 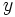 se acercan a
se acercan a 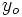 cuando la variable
cuando la variable  toma valores suficientemente grandes.
toma valores suficientemente grandes.
Simbólicamente:
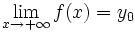
En esta escena podrás estudiar la tendencia de una función que relaciona la temperatura de un recipiente de agua que se va enfriando y el tiempo que ha transcurrido.
Estudia la tendencia del crecimiento de una población de búhos:
En ocasiones nos interesa saber cómo se comporta la función cuando la variable independiente aumenta mucho o disminuye mucho o cuando se acerca a una valor concreto. A los valores a los que se aproxima es lo que llamamos tendencia de la función. Observa la gráfica de la población de búhos (en miles) en un territorio en función del tiempo. Mueve el punto P para ayudarte a contestar las preguntas:
a) ¿Cuál es ese valor? (Nota: En el eje Y, 1 cuadrito = 1 millar de búhos)
Lo mismo ocurre cuando se hace cada vez más negativa la variable independiente, aunque esta tendencia no es el mismo valor.
b) ¿Cuál es ese valor?
Estudia la tendencia de la siguiente función:
La tendencia de una función se estudiar también cuando la x se acerca a un número real en vez de a (+/-)infinito. En la escena siguiente recorre la función con el punto P y apunta en tu cuaderno las tendencias de la función.
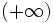 ?
?
b) ¿Y si x se hace muy grande negativamente, es decir, se aproxima a 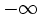 ?
?
c) ¿A qué valor tiende la función cuando nos aproximamos a 2?
Estudio de las tendencias de una función a partir de su gráfica.
Estudio de las tendencias de una función a partir de su gráfica.
Estudio de las tendencias de una función a partir de su gráfica.
Estudio de las tendencias de una función a partir de su gráfica.
|
Actividad: Tendencia de una función
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Ejercicio Resuelto: Tendencia de una función
1. Compramos un coche por 12.000 €, y cada año que pasa su precio se devalua un 20%.
- a) Haz una tabla que exprese el precio del coche durante los próximos años.
- b) Representa gráficamente los resultados del apartado a).
- c) Encuentra una fórmula que exprese esta función.
- d) ¿Cómo es la variable independiente: continua o discreta?
- e) ¿Cuál es el dominio de esta función?. ¿Y su imagen?
- f) ¿Cual es la tendencia de esta función segun pasan los años?
- g) Describe el crecimiento e indica si tiene máximos o mínimos.
- a) Tabla de valores:
| x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 12.000 | 9.600 | 7.680 | 6.144 | 4.915,2 | 3.932,2 | 3.145,7 | 2.516,6 |
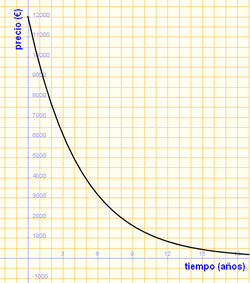
- b) Representación gráfica:
- c) Continua.
- d)
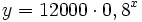 (€)
(€)
- e)
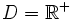 ;
; 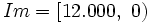 .
.
- f) La función tiende a 0 a medida que transcurre el tiempo.
- g) Es decreciente en todo su dominio. Tiene un máximo en x = 0 y no tiene mínimos.
- h) No es periódica.
Periodicidad
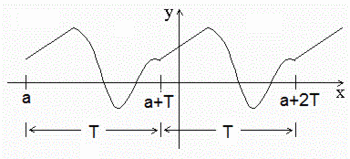
Una función es periódica si su gráfica se va repitiendo a intervalos. Al menor valor posible, T, de la longitud de dicho intervalo, se le llama periodo. Se cumple: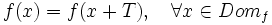 |
Actividades con las que aprenderás a determinar si una función es periódica y a hallar su período a partir de su gráfica.
|
Actividad: Funciones periódicas
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Estudio de la periodicidad de una función dada por una gráfica.
Ejercicios propuestos
|
Ejercicios propuestos: Las funciones y sus gráficas |
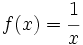 . cuando
. cuando