Plantilla:Algoritmo de Euclides

(Diferencia entre revisiones)

Revisión de 10:25 9 ago 2017

Proposición

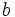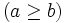Sean $a\;$ y $b\;$ , $(a \ge b)\;$ , dos números naturales, entonces se cumple que:

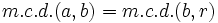
$m.c.d.(a,b)=m.c.d.(b,r)\;$

donde 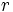$r\;$ es el resto de la división de $a\;$ entre $b\;$ .

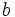Apoyándonos en el resultado anterior tenemos el siguiente algoritmo para el cáculo del m.c.d. de dos números.

Algoritmo de Euclides

El algoritmo de Euclides es un procedimiento para calcular el m.c.d. de dos números. Los pasos son:

Se divide el número mayor entre el menor.

Si la división es exacta, el divisor es el m.c.d.
Si la división no es exacta, dividimos el divisor entre el resto obtenido y se continúa de esta forma hasta obtener una división exacta, siendo el último divisor el m.c.d.

El algoritmo de Euclides

Tutorial 1 (5'43") Sinopsis:

Cálculo del m.c.d. usando el algoritmo de Euclides.

Tutorial 2 (4'45") Sinopsis:

Tutorial 3 (3'31") Sinopsis:

Cálculo del m.c.d. y del m.c.m. usando el algoritmo de Euclides.

Ejercicio 1 (6'00") Sinopsis:

Calcula el m.c.d. de 364 y 748 usando el algoritmo de Euclides.

Ejercicio 2 (4'15") Sinopsis:

Calcula el m.c.d. de 136 y 48 usando el algoritmo de Euclides.

Autoevaluación: Algoritmo de Euclides Descripción:

Ejercicios de autoevaluación sobre el algoritmo de Euclides.

-{{Teorema_sin_demo|titulo=Teorema|enunciado=
+{{Teorema_sin_demo|titulo=Proposición|enunciado=
 Sean <math>a\;</math> y <math>b\;</math>, <math>(a \ge b)\;</math>, dos números naturales, entonces se cumple que:
 }}
 {{p}}
-Apoyándonos en el anterior teorema tenemos el siguiente algoritmo para el cáculo del m.c.d. de dos números.
+Apoyándonos en el resultado anterior tenemos el siguiente algoritmo para el cáculo del m.c.d. de dos números.
 {{p}}
 {{Teorema_sin_demo|titulo=Algoritmo de Euclides|enunciado=