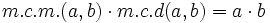Plantilla:M.c.d y propiedades
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 11:30 8 ago 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 3: | Línea 3: | ||
| {{p}} | {{p}} | ||
| {{Teorema_sin_demo|titulo=Propiedades|enunciado= | {{Teorema_sin_demo|titulo=Propiedades|enunciado= | ||
| - | *Si ''a'' es múltiplo de ''b'', entonces ''m.c.d.''(''a,b'')=''b''. | + | *Si <math>a\;</math> es múltiplo de <math>b\;</math>, entonces <math>m.c.d.(a,b)=b\;</math>. |
| - | *Los divisores comunes de varios números coinciden con los divisores del máximo común divisor. | + | *Los divisores comunes de varios números coinciden con los divisores del m.c.d. |
| - | *Dados varios números, si se multiplican o dividen por otro número entonces su m.c.d también queda multiplicado o dividido por el mismo número. | + | *Dados varios números, si se multiplican o dividen por otro número, entonces su m.c.d también queda multiplicado o dividido por el mismo número. |
| + | *Dados dos números naturales, <math>a\;</math> y <math>b\;</math>, se cumple: | ||
| + | |||
| + | <center><math>m.c.m.(a,b) \cdot m.c.d (a,b)=a \cdot b</math></center> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Ejemplo_simple|titulo=Ejemplo|contenido= | + | {{Ejemplo_simple|titulo=Ejemplos|contenido= |
| - | :m.c.d.(15, 30)=15, porque 30 es múltiplo de 15.}} | + | *Un ejemplo de la primera propiedad: |
| + | |||
| + | :m.c.d.(15, 30) = 15, porque 30 es múltiplo de 15. | ||
| + | *Un ejemplo de la última propiedad: | ||
| + | |||
| + | :m.c.d.(6,20) = 2{{b}} y{{b}} m.c.m.(6,20) = 60 | ||
| + | :m.c.m.(6,20) · m.c.d.(6,20) = 2 · 60 = '''120''' | ||
| + | :a · b = 6 · 20 = '''120'''. | ||
| + | }} | ||
Revisión actual
El máximo común divisor (m.c.d.) de dos o más números es el mayor de todos los divisores comunes a esos números.
Propiedades
- Si
 es múltiplo de
es múltiplo de 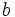 , entonces
, entonces 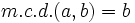 .
.
- Los divisores comunes de varios números coinciden con los divisores del m.c.d.
- Dados varios números, si se multiplican o dividen por otro número, entonces su m.c.d también queda multiplicado o dividido por el mismo número.
- Dados dos números naturales,
 y
y 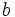 , se cumple:
, se cumple: