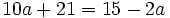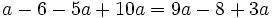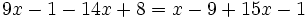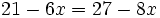Plantilla:Resolución de ecuaciones en casos más generales
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:17 11 sep 2017 Coordinador (Discusión | contribuciones) (→Actividades y videotutoriales) ← Ir a diferencia anterior |
Revisión de 18:18 11 sep 2017 Coordinador (Discusión | contribuciones) (→Actividades y videotutoriales) Ir a siguiente diferencia → |
||
| Línea 128: | Línea 128: | ||
| ==Actividades y videotutoriales== | ==Actividades y videotutoriales== | ||
| - | {{Videotutoriales|titulo=Resolución de ecuaciones de primer grado con una incógnita|enunciado= | + | {{Actividades y videotutoriales ecuaciones 1ºESO}} |
| - | {{Video_enlace_tutomate | + | |
| - | |titulo1=Ecuaciones sin paréntesis | + | |
| - | |duracion=9'00" | + | |
| - | |sinopsis=Ejemplos de resolución de ecuaciones de primer grado sencillas y más generales. | + | |
| - | |url1=https://www.youtube.com/watch?v=nrhq1pBoby0&index=4&list=PLWRbPOo5oaTcOfNT053lPqygv7Wx5PIwY | + | |
| - | }} | + | |
| - | {{Video_enlace_tutomate | + | |
| - | |titulo1=Ecuaciones con paréntesis | + | |
| - | |duracion=9'27" | + | |
| - | |sinopsis=Ejemplos de resolución de ecuaciones de primer grado con paréntesis. | + | |
| - | |url1=https://www.youtube.com/watch?v=H7lR7KkSM7Y&list=PLWRbPOo5oaTcOfNT053lPqygv7Wx5PIwY&index=5 | + | |
| - | }} | + | |
| - | {{Video_enlace_tutomate | + | |
| - | |titulo1=Ecuaciones con denominadores | + | |
| - | |duracion=8'19" | + | |
| - | |sinopsis=Ejemplos de resolución de ecuaciones de primer grado con denominadores. | + | |
| - | |url1=https://www.youtube.com/watch?v=to27Vpf8WRo&list=PLWRbPOo5oaTcOfNT053lPqygv7Wx5PIwY&index=6 | + | |
| - | }} | + | |
| - | {{Video_enlace_tutomate | + | |
| - | |titulo1=Ecuaciones con paréntesis y denominadores | + | |
| - | |duracion=9'04" | + | |
| - | |sinopsis=Ejemplos de resolución de ecuaciones de primer grado con denominadores. | + | |
| - | |url1=https://www.youtube.com/watch?v=nZ9NjJU2P2c&index=7&list=PLWRbPOo5oaTcOfNT053lPqygv7Wx5PIwY | + | |
| - | }} | + | |
| - | ---- | + | |
| - | {{Tabla50|celda1= | + | |
| - | {{Video_enlace_paps | + | |
| - | |titulo1=Ejercicio 1 | + | |
| - | |duracion=3'29" | + | |
| - | |sinopsis=Resuelve: | + | |
| - | + | ||
| - | a) <math>5x-8=3x+20\;</math> | + | |
| - | + | ||
| - | b) <math>5x+15=35\;</math> | + | |
| - | + | ||
| - | c) <math>4x=12\;</math>|url1=https://www.youtube.com/watch?v=LxLlSyKykM4 | + | |
| - | }} | + | |
| - | {{Video_enlace_julioprofe | + | |
| - | |titulo1=Ejercicio 2 | + | |
| - | |duracion=5'13" | + | |
| - | |sinopsis=Resuelve: | + | |
| - | + | ||
| - | a) <math>5a-1=14\;</math> | + | |
| - | + | ||
| - | b) <math>5x-9=3(x-2)\;</math> | + | |
| - | + | ||
| - | c) <math>4x-8=-4(2x-3)+4\;</math> | + | |
| - | |url1=https://www.youtube.com/watch?v=qeKEA066OSs&list=PL9B9AC3136D2D4C45&index=26 | + | |
| - | }} | + | |
| - | {{Video_enlace_unicoos | + | |
| - | |titulo1=Ejercicio 3 | + | |
| - | |duracion=11'44" | + | |
| - | |sinopsis=Resuelve: | + | |
| - | + | ||
| - | a) <math>8x+36=2x\;</math> | + | |
| - | + | ||
| - | b) <math>2(x-2)=2x-4\;</math> | + | |
| - | + | ||
| - | c) <math>3x+2=3x\;</math> | + | |
| - | + | ||
| - | d) <math>\cfrac{x}{2}+10=9\;</math> | + | |
| - | + | ||
| - | e) <math>\cfrac{x-3}{4}=x\;</math> | + | |
| - | |url1=http://www.unicoos.com/video/matematicas/1-eso/expresiones-algebraicas/ecuaciones-de-primer-grado/ecuaciones-de-primer-grado-01 | + | |
| - | }} | + | |
| - | {{Video_enlace_julioprofe | + | |
| - | |titulo1=Ejercicio 4 | + | |
| - | |duracion=2'48" | + | |
| - | |sinopsis=Resuelve la ecuación: <math>5x-7=-2(3-8x)+1\;</math> | + | |
| - | |url1=https://www.youtube.com/watch?v=xeUWLZY4roM&list=PL9B9AC3136D2D4C45&index=27 | + | |
| - | }} | + | |
| - | {{Video_enlace_julioprofe | + | |
| - | |titulo1=Ejercicio 5 | + | |
| - | |duracion=2'42" | + | |
| - | |sinopsis=Resuelve la ecuación: <math>-5(p-2)+3p=6(p-4)\;</math> | + | |
| - | |url1=https://www.youtube.com/watch?v=LD2VeoX0J4A&list=PL9B9AC3136D2D4C45&index=28 | + | |
| - | }} | + | |
| - | |celda2= | + | |
| - | {{Video_enlace_julioprofe | + | |
| - | |titulo1=Ejercicio 6 | + | |
| - | |duracion=3'15" | + | |
| - | |sinopsis=Resuelve la ecuación: <math>-(-2x+5)=-2(x+4)+19\;</math> | + | |
| - | |url1=https://www.youtube.com/watch?v=h4gt8tsVJbw&list=PL9B9AC3136D2D4C45&index=29 | + | |
| - | }} | + | |
| - | {{Video_enlace_clasematicas | + | |
| - | |titulo1=Ejercicio 7 | + | |
| - | |duracion=17'34" | + | |
| - | |sinopsis=Resuelve: | + | |
| - | + | ||
| - | a) <math>x-4=8\;</math> | + | |
| - | + | ||
| - | b) <math>3x=21\;</math> | + | |
| - | + | ||
| - | c) <math>\cfrac{x}{4}=7\;</math> | + | |
| - | + | ||
| - | d) <math>3x+5=11\;</math> | + | |
| - | + | ||
| - | e) <math>6x-4=3x+2\;</math> | + | |
| - | + | ||
| - | f) <math>\cfrac{x}{4}+5=3\;</math> | + | |
| - | + | ||
| - | g) <math>4x-2x-4+x=6-3x-1\;</math> | + | |
| - | + | ||
| - | h) <math>2x-4=(x+1)-1\;</math> | + | |
| - | + | ||
| - | i) <math>8-(x-4)=9\;</math> | + | |
| - | + | ||
| - | |url1=https://www.youtube.com/watch?v=sa-wcWIkz8o&index=1&list=PLZNmE9BEzVImQnTPBs51x5IR2UdM3SHF1 | + | |
| - | }} | + | |
| - | {{Video_enlace_clasematicas | + | |
| - | |titulo1=Ejercicio 8 | + | |
| - | |duracion=11'05" | + | |
| - | |sinopsis=Resuelve: | + | |
| - | + | ||
| - | a) <math>3(6+x)=2(x-6)\;</math> | + | |
| - | + | ||
| - | b) <math>-(x-1)=(x+1)-1\;</math> | + | |
| - | + | ||
| - | c) <math>8-3(2-x)=-7\;</math> | + | |
| - | + | ||
| - | |url1=https://www.youtube.com/watch?v=71qcp9DpzP0&index=2&list=PLZNmE9BEzVImQnTPBs51x5IR2UdM3SHF1 | + | |
| - | }} | + | |
| - | {{Video_enlace_clasematicas | + | |
| - | |titulo1=Ejercicio 9 | + | |
| - | |duracion=9'20" | + | |
| - | |sinopsis=Resuelve: | + | |
| - | + | ||
| - | a) <math>-2(x+1)+5(x-2)=x\;</math> | + | |
| - | + | ||
| - | b) <math>x=2(2x+5)-(3x+10)\;</math> | + | |
| - | + | ||
| - | c) <math>2(x+1)-3(x-2)=x+6\;</math> | + | |
| - | + | ||
| - | |url1=https://www.youtube.com/watch?v=lE73xT6a8WQ&list=PLZNmE9BEzVImQnTPBs51x5IR2UdM3SHF1&index=3 | + | |
| - | }} | + | |
| - | {{Video_enlace_clasematicas | + | |
| - | |titulo1=Ejercicio 10 | + | |
| - | |duracion=8'18" | + | |
| - | |sinopsis=Resuelve: | + | |
| - | + | ||
| - | a) <math>x+\cfrac{x}{2}+\cfrac{x}{3}=11\;</math> | + | |
| - | + | ||
| - | b) <math>\cfrac{x}{2}+\cfrac{3x}{4}-\cfrac{5x}{6}=15\;</math> | + | |
| - | + | ||
| - | c) <math>\cfrac{3x}{10}=\cfrac{x-1}{5}+2\;</math> | + | |
| - | + | ||
| - | |url1=https://www.youtube.com/watch?v=1rbwzgyFx20&list=PLZNmE9BEzVImQnTPBs51x5IR2UdM3SHF1&index=4 | + | |
| - | }} | + | |
| - | }} | + | |
| - | }} | + | |
| - | {{p}} | + | |
| - | + | ||
| - | {{AI_anaya|titulo1=Autoevaluación: ''Resolución de ecuaciones'' | + | |
| - | |descripcion= | + | |
| - | + | ||
| - | <center><iframe> | + | |
| - | url=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/10/06.htm | + | |
| - | width=800 | + | |
| - | height=650 | + | |
| - | name=myframe | + | |
| - | </iframe></center> | + | |
| - | + | ||
| - | |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/10/06.htm | + | |
| - | }} | + | |
Revisión de 18:18 11 sep 2017
Procedimiento
Para resolver ecuaciones de primer grado con una incógnita transformaremos la ecuación de partida en otra equivalente, más sencilla, por medio de los siguientes recursos:
- Reduciendo sus miembros, es decir, agrupando términos semejantes.
- Trasponiendo términos, esto es, utilizando las técnicas para casos sencillos vistas en los apartados anteriores.
Actividades en la que aprenderás y practicarás la resolución de ecuaciones de primer grado.
Practica la resolución de ecuaciones de primer grado.
Resolución de ecuaciones con paréntesis y/o denominadores
Procedimiento
- En el caso de que la ecuación presente paréntesis, éstos se efectuarán en primer lugar.
- En el caso de que algunos de los términos de la ecuación tengan denominador, todos los términos de la ecuación se multiplicarán por el m.c.m. de dichos denominadores.
Actividades y videotutoriales
Resuelve:
a) 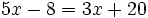
b) 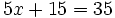
c) 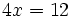
Resuelve:
a) 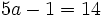
b) 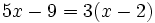
c) 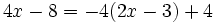
Resuelve:
a) 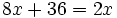
b) 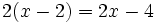
c) 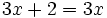
d) 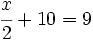
e) 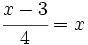
Resuelve:
a) 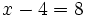
b) 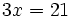
c) 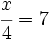
d) 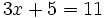
e) 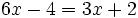
f) 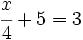
g) 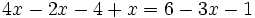
h) 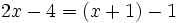
i) 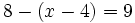
Repaso de resolución de ecuaciones de primer grado.