Plantilla:Def m.c.m.
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:05 3 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| {{Caja Amarilla|texto= | {{Caja Amarilla|texto= | ||
| - | El '''mínimo común múltiplo''' (m.c.m.) de dos o más números, es el menor de todos los múltiplos comunes a esos números.}} | + | El '''mínimo común múltiplo''' (m.c.m.) de dos o más números, es el menor de todos los múltiplos comunes a esos números, distinto de cero.}} |
| {{p}} | {{p}} | ||
| - | {{Teorema_sin_demo|titulo=Cálculo del mínimo común múltiplo | + | {{Teorema_sin_demo|titulo=Propiedad|enunciado= |
| - | |enunciado=:Para obtener el m.c.m. de dos o más números, se descomponen los números en factores primos y se toman todos los factores elevados al mayor exponente.}} | + | |
| {{p}} | {{p}} | ||
| - | {{Ejemplo_simple | + | *Si a es múltiplo de b, entonces <math>m.c.m.(a,b)=a \;\!</math>. |
| - | |titulo=Ejemplo: | + | *Los múltiplos comunes de varios números son también múltiplos del m.c.m. |
| - | |contenido= | + | *Cualquier múltiplo del m.c.m. de varios números también lo es de dichos números. |
| - | :'''Calcula el m.c.m.(24,60):''' | + | *Dados varios números, si se multiplican o dividen por otro número entonces su m.c.m también queda dividido o multiplicado por el mismo número. |
| - | ---------- | + | |
| - | :'''Primer método:''' | + | |
| - | + | ||
| - | :''Múltiplos de 24:''{{b4}}24, 48, 72, 96, '''120''', 144,... | + | |
| - | :''Múltiplos de 60:''{{b4}}60, '''120''', 180, ... | + | |
| - | + | ||
| - | :m.c.m.(24,60)= 120 | + | |
| - | --------- | + | |
| - | :'''Segundo método:''' | + | |
| - | + | ||
| - | :Descomponemos 24 y 60 en sus factores primos:<br> | + | |
| - | <center><math>24=2^3 \cdot 3\qquad60=2^2 \cdot 3 \cdot 5</math></center> | + | |
| - | :Multiplicando todos los factores elevados al mayor exponente: | + | |
| - | <center><math>m.c.m.(24,60)= 2^3 \cdot 3 \cdot 5=120</math></center> | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Video_enlace_julioprofe | + | {{Ejemplo_simple |
| - | |titulo1=Ejemplos | + | |titulo=Ejemplos |
| - | |duracion=12'12" | + | |contenido= |
| - | |sinopsis=Concepto de mínimo común múltiplo. Ejemplos. | + | m.c.m.(15, 30)=30, porque 30 es múltiplo de 15. |
| - | |url1=https://www.youtube.com/watch?v=kxDeTxbnk-c | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión actual
El mínimo común múltiplo (m.c.m.) de dos o más números, es el menor de todos los múltiplos comunes a esos números, distinto de cero.
Propiedad
- Si a es múltiplo de b, entonces
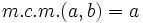 .
.
- Los múltiplos comunes de varios números son también múltiplos del m.c.m.
- Cualquier múltiplo del m.c.m. de varios números también lo es de dichos números.
- Dados varios números, si se multiplican o dividen por otro número entonces su m.c.m también queda dividido o multiplicado por el mismo número.

