Plantilla:Paso de decimal a fraccion
De Wikipedia
| Revisión de 11:58 19 oct 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 08:56 1 nov 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 136: | Línea 136: | ||
| |sinopsis=Halla la fracción generatriz de <math>2.\widehat{009}</math> (Método corto) | |sinopsis=Halla la fracción generatriz de <math>2.\widehat{009}</math> (Método corto) | ||
| |url1=https://www.youtube.com/watch?v=pNPbA3Wcg28&list=PLo7_lpX1yruO4oIwHQNwVzWaxe4EduGqi&index=6 | |url1=https://www.youtube.com/watch?v=pNPbA3Wcg28&list=PLo7_lpX1yruO4oIwHQNwVzWaxe4EduGqi&index=6 | ||
| + | }} | ||
| + | {{Video_enlace_escuela | ||
| + | |titulo1=Ejercicio 8 | ||
| + | |duracion=11'14" | ||
| + | |sinopsis=Halla la fracción generatriz por el método corto de: | ||
| + | |||
| + | <math>a) \ 2.\widehat{3} \, ; \, b) \ 3.\widehat{2} \, ; \, c) \ 0.\widehat{1} \, ; \, d) \ 0.\widehat{4} \, ; \, e) \ 3.\widehat{21} \, ; \, f) \ 2.\widehat{34} \, ; \, g) \ 0.\widehat{25} \, ; \, h) \ 0.\widehat{26} \, ; \,</math> | ||
| + | |||
| + | <math> i) \ 1.\widehat{05} \, ; \, j) \ 2.\widehat{36} \, ; \, k) \ 0.\widehat{27} \, ; \, l) \ 0.\widehat{36} \, ; \, m) \ 1.\widehat{32} \, ; \, n) \ 2.\widehat{34} \, ; \, o) \ 3.\widehat{35}</math> | ||
| + | |url1=https://www.youtube.com/watch?v=rd8xAunKOdI&index=5&list=PLw7Z_p6_h3oxzoTBCiwpDlYrXOPOKXuQA | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 08:56 1 nov 2017
- Actividad en la que podrás ver como se obtiene la fracción generatriz de una expresión decimal exacta, periódica pura o periódica mixta.
- Actividad en la que tendrás que hallar la fracción generatriz de una expresión decimal.
Cómo obtener la fracción generatiz de un número decimal exacto o periódico (2 métodos) con ejemplos:
1. a) 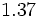 b)
b) 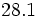 c)
c) 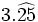 d)
d) 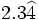
2. a) 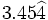 b)
b) 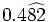 c)
c) 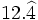
Tutorial en el que se da un rápido repaso a los distintos tipos de decimales y se explica el paso de un número en expresión decimal a su expresión fraccionaria equivalente, tanto en el caso de decimales finitos como periódicos.
Paso de decimal exacto a fracción
La fracción generatriz de un decimal exacto tiene en el numerador la expresión decimal sin la coma, y en el denominador un uno seguido de tantos ceros como cifras decimales.
Es consecuencia del siguiente procedimiento:
- Sea N el número decimal exacto.
- Multiplicamos N por 10 elevado al número de decimales.
- Despejamos N para obtener la fracción.
Paso de decimal exacto a fracción y su simplificación.
Cómo obtener la fracción generatiz de un número decimal exacto. Ejemplos.
Halla la fracción generatriz de 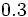
Halla la fracción generatriz de 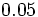
Halla la fracción generatriz de 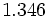
Halla la fracción generatriz de los números:
- a)
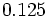
- b)
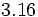
Halla la fracción generatriz de los números:
- a)
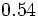 ; b)
; b) 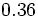 ; c)
; c) 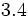 ; d)
; d) 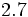 ; e)
; e) 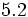 ; f)
; f) 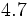 ; g)
; g) 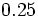 ; h)
; h) 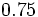 ; i)
; i) 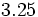 ; j)
; j) 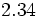 ; k)
; k) 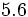 ; l)
; l) 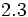 ;
;
Transforma en fracción los siguientes números decimales exactos:
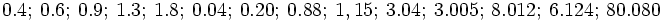
Halla la fracción generatriz de 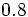
Halla la fracción generatriz de 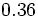
Halla la fracción generatriz de 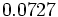
Halla la fracción generatriz de 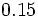
Convierte en número mixto 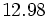
Actividad en la que debes pasar de decimal exacto a fracción.
Paso de decimal periódico puro a fracción
La fracción generatriz de un número decimal periódico puro tiene como numerador la diferencia entre a y b, donde a es el número escrito sin la coma (sin repetir el periodo) y b es la parte entera del número; y como denominador, tantos "9" como cifras tiene el periodo.
Es consecuencia del siguiente procedimiento:
- Sea N el número decimal.
- Multiplicamos N por 10 elevado al número de cifras que tenga el periodo, lo que permite obtener otro número con la misma parte decimal.
- Restamos N y el número obtenido en el paso anterior.
- Despejando N llegamos a la fracción buscada.
Halla la fracción generatriz de los números periódicos puros (2 métodos):
- a) 1.6666...
- b) 2.646464...
Halla la fracción generatriz de número periódico puro 0.3636... (Método largo)
Halla la fracción generatriz de los siguientes números periódicos puros (Método corto):
- a) 0.888...
- b) 0.212121...
- c) 0.537537537...
- d) 2.444...
- e) 10.484848...
Halla la fracción generatriz de los números (Método corto):
- a) 0.363636...
- b) 2.045045...
Halla la fracción generatriz de 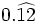 (Método corto)
(Método corto)
Halla la fracción generatriz de 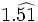 (Método corto)
(Método corto)
Halla la fracción generatriz de 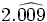 (Método corto)
(Método corto)
Halla la fracción generatriz por el método corto de:
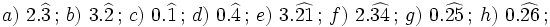
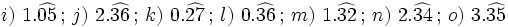
Actividad en la que debes pasar de decimal periódico puro a fracción.
Paso de decimal periódico mixto a fracción
La fracción generatriz de un número decimal periódico mixto tiene como numerador la diferencia entre a y b, donde a es el número escrito sin la coma (sin repetir el periodo) y b es el número escrito sin la coma quitándole la parte decimal periódica. El denominador tendrá tantos "9" como cifras tiene el periodo y otros tantos "0" como cifras tenga el anteperiodo.
Es consecuencia del siguiente procedimiento:
- Sea N el número decimal.
- Multiplicamos N por 10 elevado al número de cifras que tenga el periodo más el anteperiodo.
- Multiplicamos N por 10 elevado al número de cifras que tenga el anteperiodo, lo que permite obtener otro número con la misma parte decimal que el del paso 2.
- Restamos los números obtenidos en los pasos 2 y 3.
- Despejando N llegamos a la fracción buscada.
Halla la fracción generatriz de los siguientes números periódicos mixtos (2 métodos):
- a) 2.46666...
- b) 3.246262626...
Halla la fracción generatriz de número periódico mixto 0.4333... (Método largo)
Halla la fracción generatriz de los siguientes números periódicos mixtos (Método corto):
- a) 0.5111...
- b) 0.935555...
- c) 3.8121212...
- d) 1.06434343...
Halla la fracción generatriz de los siguientes números periódicos mixtos (Método corto):
- a) 0.3851851...
- b) 4.1244444...
Halla la fracción generatriz de 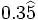 (Método corto)
(Método corto)
Halla la fracción generatriz de 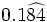 (Método corto)
(Método corto)
Halla la fracción generatriz de 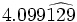 (Método corto)
(Método corto)
Actividad en la que debes pasar de decimal periódico mixto a fracción.
Ejercicios de autoevaluación sobre fracciones generatrices.

