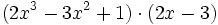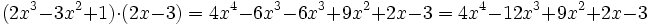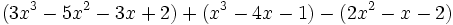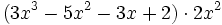Plantilla:Producto de polinomios
De Wikipedia
| Revisión de 09:22 5 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 08:02 6 nov 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 98: | Línea 98: | ||
| |titulo1=Ejercicio 5 | |titulo1=Ejercicio 5 | ||
| |duracion=7'34" | |duracion=7'34" | ||
| - | |sinopsis=1 ejercicio | + | |sinopsis=Dados los polinomios |
| + | |||
| + | :<math>A(x)=x^3-3x^2+2\;</math> ; {{b4}}<math>B(x)=2x^2-x\;</math> ; {{b4}}<math>C(x)=x^3-2x^2\;</math> | ||
| + | |||
| + | determina: | ||
| + | |||
| + | :a) A(x)· B(x) | ||
| + | :b) C(x)· [A(x)+ B(x)] | ||
| + | |||
| |url1=https://www.youtube.com/watch?v=lHMdgx4KY1k&list=PL54E0E2B3C3F7EA2B&index=5 | |url1=https://www.youtube.com/watch?v=lHMdgx4KY1k&list=PL54E0E2B3C3F7EA2B&index=5 | ||
| }} | }} | ||
| Línea 104: | Línea 112: | ||
| |titulo1=Ejercicio 6 | |titulo1=Ejercicio 6 | ||
| |duracion=9'59" | |duracion=9'59" | ||
| - | |sinopsis=Ejercicio 3: Multiplicar polinomios en columna e indicar el grado del producto. | + | |sinopsis=Multiplica los siguientes polinomios en columna e indicar el grado de los factores y del producto. |
| + | |||
| + | :3a) <math>(2x^2-4x+6) \cdot \left( \cfrac{1}{2}x+1 \right)\;</math> | ||
| + | :3b) <math>(x^3+5x-2) \cdot (2x^2+1)\;</math> | ||
| + | :3c) <math>(2x^4+3x^3-x^2+4x+2) \cdot (2x^2+3x-1)\;</math> | ||
| + | |||
| |url1=https://www.youtube.com/watch?v=RoawrRxC0P0&list=PLw7Z_p6_h3oxU1jHlHchenHoWdC0XkGCi&index=7 | |url1=https://www.youtube.com/watch?v=RoawrRxC0P0&list=PLw7Z_p6_h3oxU1jHlHchenHoWdC0XkGCi&index=7 | ||
| }} | }} | ||
Revisión de 08:02 6 nov 2017
Procedimiento
Para multiplicar dos polinomios, se multiplica cada monomio de uno de sus factores por todos y cada uno de los monomios del otro factor y, después, se suman los monomios semejantes obtenidos.
Aprende a multiplicar binomios
Aprende a multiplicar polinomios
En este tutorial se explica la multiplicación de monomios y polinomios comenzando con algunas definiciones básicas y terminando con ejemplos.
Producto de monomios y polinomios en una variable.
Cómo se multiplican polinomios.
Propiedades conmutativa y asociativa del producto de polinomios.
Elemento neutro y distributiva en el producto de polinomios.
Multiplica:
- a)
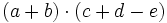
- b)
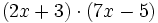
- c)
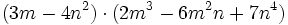
- d)
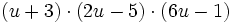
Multiplica:
- a)
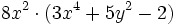
- b)
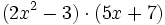
- c)
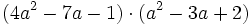
Determinar el polinomio que tiene por raíces: 2, 3 y -1, siendo la última raíz de multiplicidad 2.
Haz las siguientes multiplicaciones de polinomios:
- a)
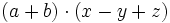
- b)
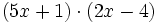
- c)
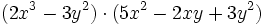
- d)
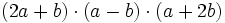
Dados los polinomios
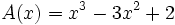 ;
; 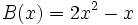 ;
; 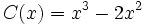
determina:
- a) A(x)· B(x)
- b) C(x)· [A(x)+ B(x)]
Multiplica los siguientes polinomios en columna e indicar el grado de los factores y del producto.
- 3a)
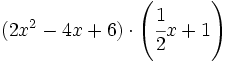
- 3b)
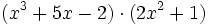
- 3c)
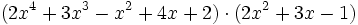
Ejercicio 4: Comprobar las propiedades del producto de polinomios.
Ejercicios 5 -6a: Aplicar el elemento neutro y la conmutativa al producto de polinomios.
Ejercicio 6b: Aplicar la propiedad asociativa al producto de polinomios.
Ejercicio 7a: Comprobar la propiedad distributiva del producto respecto a la suma de polinomios.
Ejercicio 7b: Calcular el cuadrado de un polinomio.
Ejercicios 8a-e: Calcular el producto de polinomios.
Ejercicios 8f-h: Calcular cuadrados y productos de polinomios.
Ejercicio 9: Multiplicar dos polinomios.
Ejercicio 10: Calcular el producto de dos binomios.
Actividades para aprender y practicar la multiplicación de polinomios.
Ejercicios de autoevaluación sobre producto de de polinomios.
|
Actividad: Operaciones con polinomios Haz las siguientes operaciones con polinomios:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: a) expand (3x^3-5x^2-3x+2)+(x^3-4x-1)-(2x^2-x-2) b) expand (3x^3-5x^2-3x+2)*2x^2 c) expand (2x^2+2x-3)*(2x-5) |