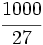Plantilla:Videos: Potencia de un racional
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 11:22 11 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 17: | Línea 17: | ||
| }} | }} | ||
| {{Video_enlace_virtual | {{Video_enlace_virtual | ||
| - | |titulo1=Potencia de exponente cero | + | |titulo1=Tutorial 2: ''Potencia de exponente cero'' |
| |duracion=1'35" | |duracion=1'35" | ||
| |sinopsis=<math>a^0 = 1 \ , \ \forall a \ne 0\;</math>. Ejemplos. | |sinopsis=<math>a^0 = 1 \ , \ \forall a \ne 0\;</math>. Ejemplos. | ||
| Línea 24: | Línea 24: | ||
| ---- | ---- | ||
| {{Video_enlace_escuela | {{Video_enlace_escuela | ||
| - | |titulo1=Ejercicio | + | |titulo1=Ejercicios |
| |duracion=10'51" | |duracion=10'51" | ||
| - | |sinopsis=Ejercicios 1 al 10: Operaciones básicas con potencias de fracciones. | + | |sinopsis= |
| + | *Escribe en forma de potencia los siguientes productos: | ||
| + | |||
| + | :1) <math>\cfrac{1}{2} \cdot \cfrac{1}{2} \cdot \cfrac{1}{2}\;</math> | ||
| + | |||
| + | :2) <math>\cfrac{-3~}{5} \cdot \cfrac{-3~}{5} \cdot \cfrac{-3~}{5} \cdot \cfrac{-3~}{5}\;</math> | ||
| + | |||
| + | :3) <math>\cfrac{2}{3} \cdot\cfrac{2}{3} \cdot\cfrac{2}{3} \cdot\cfrac{2}{3} \cdot\cfrac{2}{3}\;</math> | ||
| + | |||
| + | {{p}} | ||
| + | |||
| + | *Escribe en forma de una única potencia: | ||
| + | |||
| + | :4) <math>\cfrac{6^7}{6^3}\;</math>; {{b4}}{{b4}} 5) <math>\cfrac{5^9}{5}\;</math> ; {{b4}}{{b4}} 6) <math>\cfrac{12^2}{12^0}\;</math> | ||
| + | |||
| + | :7) <math>\cfrac{25}{16}\;</math> ; {{b4}}{{b4}} 8) <math>\cfrac{3^2}{5^2}\;</math> ; {{b4}}{{b4}} 9) <math>\cfrac{9}{4}\;</math> ; {{b4}}{{b4}} 10) <math>\cfrac{1000}{27}\;</math> | ||
| |url1=https://www.youtube.com/watch?v=3sUY1n3iWEo&list=PLw7Z_p6_h3oxskBUdR5nmGa6YMySFNSY-&index=9 | |url1=https://www.youtube.com/watch?v=3sUY1n3iWEo&list=PLw7Z_p6_h3oxskBUdR5nmGa6YMySFNSY-&index=9 | ||
| }} | }} | ||
| }} | }} | ||
Revisión actual
- Breve repaso de las potencias de base entera y exponente natural.
- Potencias de base racional y exponente natural.
- Potencias de exponente 0 y 1.
Cómo se calcula la potencia de una fracción. Ejemplos.
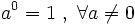 . Ejemplos.
. Ejemplos.
- Escribe en forma de potencia los siguientes productos:
- 1)
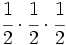
- 2)
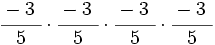
- 3)
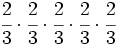
- Escribe en forma de una única potencia:
- 4)
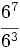 ; 5)
; 5) 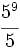 ; 6)
; 6) 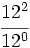
- 7)
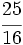 ; 8)
; 8) 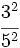 ; 9)
; 9) 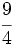 ; 10)
; 10)