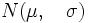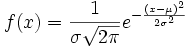La distribución normal
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 14:33 2 jul 2007 Juanmf (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 14:37 2 jul 2007 Juanmf (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 2: | Línea 2: | ||
| Una variable aleatoria continua sigue una distribución normal si su función de densidad es: | Una variable aleatoria continua sigue una distribución normal si su función de densidad es: | ||
| {{Caja|contenido= | {{Caja|contenido= | ||
| - | <math> f(x)= \frac{1} { \sigma \sqrt{2 \pi}e^{- \frac{(x- \mu )^2} {2 \sigma^2} </math> | + | <math> f(x)= \frac{1} { \sigma \sqrt{2 \pi}}e^{- \frac{(x- \mu )^2} {2 \sigma^2}} |
| + | </math> | ||
| }} | }} | ||
| - | donde <math> \mu \quad y \quad \sigma </math> coinciden respectivamente con la media y la desviación típica de la variable aleatoria. Estos parámetros son los que determinan esta distribución que designaremos por <math> N( \mu \quad , \quad \sigma ) </math> | + | donde <math> \mu \quad y \quad \sigma </math> coinciden respectivamente con la media y la desviación típica de la variable aleatoria. Estos parámetros son los que determinan esta distribución que designaremos por <math> N( \mu , \quad \sigma ) </math> |
| - | + | ||
| }} | }} | ||
Revisión de 14:37 2 jul 2007
Una variable aleatoria continua sigue una distribución normal si su función de densidad es:
|
|
donde 
coinciden respectivamente con la media y la desviación típica de la variable aleatoria. Estos parámetros son los que determinan esta distribución que designaremos por 
