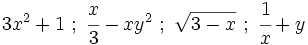Plantilla:Expresiones algebraicas
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:53 9 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | *Una '''expresión algebraica''' es cualquier combinación de letras y números ligados por las operaciones matemáticas (suma, resta, multiplicación, división, potenciación, radicación, ...). | + | *Una '''expresión algebraica''' es una combinación de letras y números ligados por las operaciones matemáticas (suma, resta, multiplicación, división, potenciación, radicación, ...), que respeta las reglas del lenguaje algebraico. |
| *Las letras, que suelen representar cantidades desconocidas, no tienen un valor fijo y se denominan '''variables'''. Los números se denominan '''constantes''' porque tienen un valor fijo. | *Las letras, que suelen representar cantidades desconocidas, no tienen un valor fijo y se denominan '''variables'''. Los números se denominan '''constantes''' porque tienen un valor fijo. | ||
| + | }} | ||
| + | {{Nota|titulo=Observación:|texto= | ||
| + | #Se puede usar cualquier letra del alfabeto para expresar una variable, excepto la "<math>e</math>" y la "<math>i</math>", porque están reservadas para unos números especiales. Las letras más habituales son ''x, y, z, a, b, c, ...'' | ||
| + | #Las reglas que se mencionan en la definición son las mismas que ya teníamos en cuenta al trabajar únicamente con números y alguna otra que aparecerá más adelante. Entre ellas tenemos: | ||
| + | |||
| + | ::*Dos símbolos de operación no pueden aparecer juntos sin estar separados por otro elemento (paréntesis, corchetes, raya de fracción...) | ||
| + | ::*Cuando realizamos una operación combinada en varias etapas, cada una de ellas tiene que estar precedida del símbolo =, y los elementos que no se operan deben repetirse en la misma posición o en una equivalente, siempre respetando las propiedades de las operaciones. | ||
| + | ::*Si el símbolo = está seguido por una raya de fracción, ésta debe aparecer a una altura intermedia entre las dos rayas del igual. | ||
| + | ::*El número 1 puede omitirse cuando está multiplicando a otro número o cuando actúa como exponente. | ||
| + | ::*El símbolo de la multiplicación puede omitirse cuando a continuación del mismo aparecen unos paréntesis, o cuando se indica el producto de dos variables (letras). | ||
| + | ::*... | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| {{Ejemplo_simple|titulo=Ejemplos:|contenido=Son expresiones algebraicas: <math>3x^2+1 \ ; \ \cfrac{x}{3}-xy^2 \ ; \ \sqrt{3-x} \ ; \ \cfrac{1}{x} +y</math> | {{Ejemplo_simple|titulo=Ejemplos:|contenido=Son expresiones algebraicas: <math>3x^2+1 \ ; \ \cfrac{x}{3}-xy^2 \ ; \ \sqrt{3-x} \ ; \ \cfrac{1}{x} +y</math> | ||
| - | }} | ||
| - | {{p}} | ||
| - | Las expresiones algebraicas nos permiten traducir al lenguaje matemático expresiones del lenguaje habitual. | ||
| - | {{p}} | ||
| - | {{Ejemplo|titulo=Ejemplos: ''Expresiones algebraicas'' | ||
| - | |enunciado= | ||
| - | Expresa mediante expresiones algebraicas: | ||
| - | |||
| - | :a) El doble de un número menos cuatro unidades. | ||
| - | :b) La mitad de sumarle 5 al triple de un número. | ||
| - | :c) El perímetro y el área de un terreno rectangular. | ||
| - | |||
| - | |sol= | ||
| - | a) Si llamamos <math>x\;\!</math> al número, entonces el doble del número menos cuatro unidades es <math>2x-4\;</math>. | ||
| - | |||
| - | b) Llamando <math>x\;\!</math> al número, la mitad de sumarle 5 al triple de dicho número es <math>\cfrac{3x+5}{2}</math> | ||
| - | |||
| - | c) Si suponemos que el terreno rectangular mide <math>x\;\!</math> de largo e <math>y\;\!</math> de ancho, tenemos: | ||
| - | |||
| - | *Perimetro: <math>2x+2y\;\!</math> | ||
| - | *Area: <math>x \cdot y</math> | ||
| - | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 45: | Línea 34: | ||
| |descripcion=Actividad en la que deberás encontrar la expresión algebraica adecuada para cada situación. | |descripcion=Actividad en la que deberás encontrar la expresión algebraica adecuada para cada situación. | ||
| |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena5/2quincena5_presenta_1a.htm | |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena5/2quincena5_presenta_1a.htm | ||
| - | }} | ||
| - | {{AI_cidead | ||
| - | |titulo1=Traducción de enunciados (I) | ||
| - | |descripcion=Actividades en la que aprenderás y practicarás la traducción de enunciados al lenguaje algebraico. | ||
| - | |url1=http://recursostic.educacion.es/secundaria/edad/1esomatematicas/1quincena7/1quincena7_contenidos_1b.htm | ||
| - | }} | ||
| - | {{AI_cidead | ||
| - | |titulo1=Traducción de enunciados (II) | ||
| - | |descripcion=Actividades en la que aprenderás y practicarás la traducción de enunciados al lenguaje algebraico. | ||
| - | |url1=http://recursostic.educacion.es/secundaria/edad/2esomatematicas/2quincena5/2quincena5_contenidos_1b.htm | ||
| - | }} | ||
| - | ---- | ||
| - | {{AI_melide | ||
| - | |titulo1=Autoevaluación 1: ''Traducción al lenguaje algebraico'' | ||
| - | |descripcion=Ejercicios de autoevaluación sobre cómo se traducen enunciados al lenguaje algebraico. | ||
| - | |url1=http://www.edu.xunta.gal/centros/iesmelide/aulavirtual2/pluginfile.php/2748/mod_imscp/content/1/lenguaje_algebraico.html | ||
| - | }} | ||
| - | {{AI_enlace | ||
| - | |titulo1=Autoevaluación 2: ''Traducción al lenguaje algebraico'' | ||
| - | |descripcion=Ejercicios de autoevaluación sobre cómo se traducen enunciados al lenguaje algebraico. | ||
| - | |url1=http://quizlet.com/189014983/learn | ||
| - | }} | ||
| - | {{AI_enlace | ||
| - | |titulo1=Autoevaluación 3: ''Traducción al lenguaje algebraico'' | ||
| - | |descripcion=Ejercicios de autoevaluación sobre cómo se traducen enunciados al lenguaje algebraico. | ||
| - | |url1=http://quizlet.com/189014983/write | ||
| - | }} | ||
| - | {{AI_enlace | ||
| - | |titulo1=Autoevaluación 4: ''Traducción al lenguaje algebraico'' | ||
| - | |descripcion=Ejercicios de autoevaluación sobre cómo se traducen enunciados al lenguaje algebraico. | ||
| - | |url1=http://quizlet.com/189014983/test | ||
| - | }} | ||
| - | {{AI_enlace | ||
| - | |titulo1=Autoevaluación 5: ''Traducción al lenguaje algebraico'' | ||
| - | |descripcion=Ejercicios de autoevaluación sobre cómo se traducen enunciados al lenguaje algebraico. | ||
| - | |url1=http://es.khanacademy.org/math/cc-sixth-grade-math/cc-6th-expressions-and-variables/cc-6th-alg-expression-word-problems/e/writing-basic-algebraic-expressions-word-problems-2 | ||
| - | }} | ||
| - | {{AI_vitutor | ||
| - | |titulo1=Autoevaluación 6: ''Traducción al lenguaje algebraico'' | ||
| - | |descripcion=Ejercicios de autoevaluación sobre cómo se traducen enunciados al lenguaje algebraico. | ||
| - | |url1=http://www.vitutor.com/ecuaciones/1/ecua30_Contenidos_e.html | ||
| }} | }} | ||
| }} | }} | ||
Revisión actual
- Una expresión algebraica es una combinación de letras y números ligados por las operaciones matemáticas (suma, resta, multiplicación, división, potenciación, radicación, ...), que respeta las reglas del lenguaje algebraico.
- Las letras, que suelen representar cantidades desconocidas, no tienen un valor fijo y se denominan variables. Los números se denominan constantes porque tienen un valor fijo.
- Se puede usar cualquier letra del alfabeto para expresar una variable, excepto la "e" y la "i", porque están reservadas para unos números especiales. Las letras más habituales son x, y, z, a, b, c, ...
- Las reglas que se mencionan en la definición son las mismas que ya teníamos en cuenta al trabajar únicamente con números y alguna otra que aparecerá más adelante. Entre ellas tenemos:
- Dos símbolos de operación no pueden aparecer juntos sin estar separados por otro elemento (paréntesis, corchetes, raya de fracción...)
- Cuando realizamos una operación combinada en varias etapas, cada una de ellas tiene que estar precedida del símbolo =, y los elementos que no se operan deben repetirse en la misma posición o en una equivalente, siempre respetando las propiedades de las operaciones.
- Si el símbolo = está seguido por una raya de fracción, ésta debe aparecer a una altura intermedia entre las dos rayas del igual.
- El número 1 puede omitirse cuando está multiplicando a otro número o cuando actúa como exponente.
- El símbolo de la multiplicación puede omitirse cuando a continuación del mismo aparecen unos paréntesis, o cuando se indica el producto de dos variables (letras).
- ...
Expresiones algebraicas: definición y ejemplos.
Expresiones algebraicas. Tipos de expresiones algebraicas: enteras y fraccionarias.
Indica si las siguientes expresiones algebraicas son enteras o fraccionarias:
- 44)
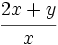 ; 45)
; 45) 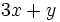 ; 46)
; 46) 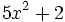
- 47)
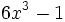 ; 48)
; 48) 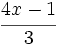 ; 49)
; 49) 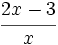
- 50)
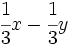
Ejemplos de expresiones algebraicas.
Actividad en la que deberás encontrar la expresión algebraica adecuada para cada situación.
Actividad en la que deberás encontrar la expresión algebraica adecuada para cada situación.