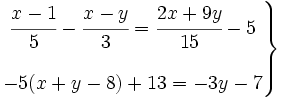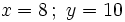Plantilla:Reglas para resolver sistemas lineales
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:14 28 dic 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 13: | Línea 13: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Actividades|titulo=Resoución de sistemas|enunciado= | ||
| - | {{AI_Khan | ||
| - | |titulo1=Autoevaluación 1a | ||
| - | |descripcion=Número de soluciones de un sistema de ecuaciones: método algebraico. | ||
| - | |url1=http://es.khanacademy.org/math/algebra/systems-of-linear-equations/possible-number-of-solutions-of-systems-of-linear-equations/e/constructing-consistent-and-inconsistent-system | ||
| - | }} | ||
| - | {{AI_Khan | ||
| - | |titulo1=Autoevaluación 1b | ||
| - | |descripcion=Número de soluciones de un sistema de ecuaciones: método algebraico. | ||
| - | |url1=http://es.khanacademy.org/math/algebra/systems-of-linear-equations/solving-any-system-of-linear-equations/e/systems_of_equations | ||
| - | }} | ||
| {{Ejercicios_vitutor | {{Ejercicios_vitutor | ||
| |titulo1=Ejercicios resueltos | |titulo1=Ejercicios resueltos | ||
| |descripcion=Ejercicios de autoevaluación sobre resolución de sistemas lineales. | |descripcion=Ejercicios de autoevaluación sobre resolución de sistemas lineales. | ||
| |url1=http://www.vitutor.com/ecuaciones/sistemas/sisActividades.html | |url1=http://www.vitutor.com/ecuaciones/sistemas/sisActividades.html | ||
| - | }} | ||
| }} | }} | ||
Revisión actual
Procedimiento
Para resolver un sistema de ecuaciones lineales podemos proceder de la siguiente forma:
- Transformar las ecuaciones del sistema hasta que tengan la forma
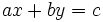. Para ello deberás quitar denominadores y paréntesis (si los hay), transponer términos y simplificar.
- Elegir un método de resolución adecuado: el método de sustitución es cómodo si alguna incógnita tiene coeficiente 1 o -1; el de reducción es cómodo si alguna incógnita tiene el mismo coeficiente en las dos ecuaciones o sus coeficientes son uno múltiplo del otro; el de igualación es cómodo por su mecánica de despejar, igualar y multiplicar en cruz.
- Podemos, opcionalmente, comprobar las soluciones. Para ello sustituiremos las incógnitas por los valores obtenidos en las dos ecuaciones del sistema de partida y los resultados deben coincidir.
Ejercicio resuelto
Resuelve el siguiente sistema:
Solución:
Solución:
Ejercicios resueltos Descripción: Ejercicios de autoevaluación sobre resolución de sistemas lineales.
