Plantilla:Valor absoluto de una función (1ºBach)

De Wikipedia

(Diferencia entre revisiones)
Revisión de 18:30 29 dic 2017
Coordinador (Discusión | contribuciones)
(→Valor absoluto de una función)
← Ir a diferencia anterior		 Revisión actual
Coordinador (Discusión | contribuciones)
(→Representación gráfica del valor absoluto de una función)
Línea 61: Línea 61:
|sinopsis=Representa gráficamente: |sinopsis=Representa gráficamente:
-:a) <math>\left| x-2 \right|</math>+:a) <math>y=\left| x-2 \right|</math>
-:b) <math>\left| 9-3x \right|</math>+:b) <math>y=\left| 9-3x \right|</math>
-:c) <math>\left| x^2-6x+5 \right|</math>+:c) <math>y=\left| x^2-6x+5 \right|</math>
|url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/3001-tres-ejercicios-3 |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/3001-tres-ejercicios-3
Línea 72: Línea 72:
|sinopsis=Representa gráficamente: |sinopsis=Representa gráficamente:
-:a) <math>x+ \left| x-2 \right|</math>+:a) <math>y=x+ \left| x-2 \right|</math>
-:b) <math>x^2 - \left| x^2-4 \right|</math>+:b) <math>y=x^2 - \left| x^2-4 \right|</math>
|url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/3002-dos-ejercicios-3 |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/3002-dos-ejercicios-3
}} }}
Línea 79: Línea 79:
|titulo1=Ejercicio 3 |titulo1=Ejercicio 3
|duracion=4'27" |duracion=4'27"
-|sinopsis=Representa gráficamente: <math>x^2 - \left| 4-x^2 \right|</math>+|sinopsis=Representa gráficamente: <math>y=x^2 - \left| 4-x^2 \right|</math>
|url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/3003-ejercicio-6 |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/15-funciones-reales-de-variable-real/3003-ejercicio-6
}} }}

Revisión actual

[editar]

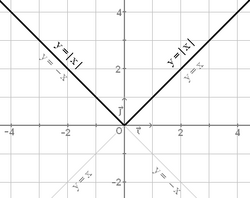
Función valor absoluto

La función valor absoluto es aquella que a cada número 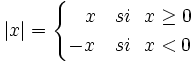x\; le asigna su valor absoluto. Es decir:  

|x|=\begin{cases} \ \ \, x & si \ \ x \ge 0 \\ -x & si \ \ x < 0 \end{cases}

Función valor absoluto     Descripción:

Representación de la función valor absoluto.

[editar]

Valor absoluto de una función

El valor absoluto de una función se define como:  

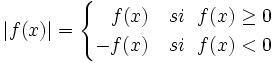
|f(x)|=\begin{cases} \ \ \, f(x) & si \ \ f(x) \ge 0 \\ -f(x) & si \ \ f(x) < 0 \end{cases}

Valor absoluto de una función (7'35")     Sinopsis:

Siendo "f" y "u" funciones reales de variable real, escribimos f = | u | si f(x) = | u(x) | .

  • La gráfica de "f" coincide con la de "u" en los puntos en que ésta toma valores no negativos.
  • En los puntos en que "u" toma valores negativos, la gráfica de "f" es simétrica de la de "u" respecto al eje de abcisas.
Valor absoluto de una función     Descripción:

Representación conjunta de una función cualquiera y su valor absoluto.

[editar]

Representación gráfica del valor absoluto de una función

ejercicio

Procedimiento

Para representar gráficamente el valor absoluto de una función f:

  1. Representamos la función f.
  2. Hacemos una simetría respecto del eje X de la parte de la gráfica de f que está por debajo de dicho eje.
  3. Borramos esa parte de f que está por debajo del eje X.
  4. La parte de la gráfica de f que está por encima del eje X la dejamos tal cual.
  5. La gráfica resultante es la gráfica del valor absoluto de f.

video
Representación gráfica del valor absoluto de una función
Ejercicio 1 (10'04")     Sinopsis:

Representa gráficamente:

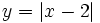
a) y=\left| x-2 \right|
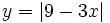
b) y=\left| 9-3x \right|
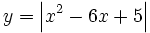
c) y=\left| x^2-6x+5 \right|
Ejercicio 2 (8'36")     Sinopsis:

Representa gráficamente:

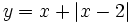
a) y=x+ \left| x-2 \right|
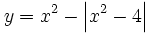
b) y=x^2 - \left| x^2-4 \right|
Ejercicio 3 (4'27")     Sinopsis:

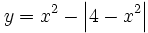
Representa gráficamente: y=x^2 - \left| 4-x^2 \right|

Ejercicio 4 (30'33")     Sinopsis:

Representa gráficamente:

a) f(x) = x + | x − 2 |
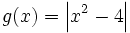
b) g(x)=\left| x^2-4 \right|
c) h(x) = | x | − x
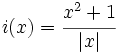
d) i(x)=\cfrac{x^2+1}{|x|}
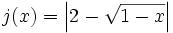
e) j(x)=\left| 2-\sqrt{1-x} \right|

Representación gráfica del valor absoluto de una función     Descripción:

Autoevaluación.

Obtenido de "http://www.maralboran.org/wikipedia/index.php/Plantilla:Valor_absoluto_de_una_funci%C3%B3n_%281%C2%BABach%29"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda