Sistemas de ecuaciones de primer grado
De Wikipedia
| Revisión de 18:16 5 jul 2007 Coordinador (Discusión | contribuciones) (→Soluciones de una ecuación de primer grado con dos incógnitas) ← Ir a diferencia anterior |
Revisión de 19:50 5 jul 2007 Coordinador (Discusión | contribuciones) (→Soluciones de una ecuación de primer grado con dos incógnitas) Ir a siguiente diferencia → |
||
| Línea 21: | Línea 21: | ||
| |enunciado= | |enunciado= | ||
| :Halla algunas soluciones para la ecuación: | :Halla algunas soluciones para la ecuación: | ||
| - | <center><math>3x+y=5\;\!</math></center> | + | <center><math>2x+3y=4\;\!</math></center> |
| |sol= | |sol= | ||
| Despejamos la variable y: | Despejamos la variable y: | ||
| - | <center><math>y=5-3x\;\!</math></center> | + | <center><math>y=\cfrac{4-2x}{3}</math></center> |
| Construimos una tabla de valores, dandole valores a <math>x\;\!</math> y calculando <math>y\;\!</math> en la expresión anterior: | Construimos una tabla de valores, dandole valores a <math>x\;\!</math> y calculando <math>y\;\!</math> en la expresión anterior: | ||
| <table border=1 align=center> | <table border=1 align=center> | ||
| <tr align=center> | <tr align=center> | ||
| <td>'''x'''</td> | <td>'''x'''</td> | ||
| - | <td>0</td> | + | <td>-1</td> |
| - | <td>1</td> | + | |
| <td>2</td> | <td>2</td> | ||
| + | <td>5</td> | ||
| <td>...</td> | <td>...</td> | ||
| </tr> | </tr> | ||
| <tr align=center> | <tr align=center> | ||
| <td>'''y'''</td> | <td>'''y'''</td> | ||
| - | <td>5</td> | + | <td>2</td> |
| - | <td>2</td> | + | <td>0</td> |
| - | <td>-1</td> | + | <td>-2</td> |
| <td>...</td> | <td>...</td> | ||
| </tr> | </tr> | ||
| </table> | </table> | ||
| Las soluciones vienen dadas por las parejas <math>(x,y)\;\!</math> así obtenidas: | Las soluciones vienen dadas por las parejas <math>(x,y)\;\!</math> así obtenidas: | ||
| - | <center><math>(0,5),\ (1,2),\ (2,-1),...</math></center> | + | <center><math>(-1,2),\ (2,0),\ (5,-2),...</math></center> |
| + | |||
| + | Compruébalas en la siguiente escena: | ||
| + | |||
| + | <center><iframe> | ||
| + | url=http://maralboran.ath.cx/web_ma/descartes/Algebra/Resolucion_grafica_sistemas_ecuaciones/Resolucion_grafica_sistemas_1.html | ||
| + | width=460 | ||
| + | height=380 | ||
| + | name=myframe | ||
| + | </iframe></center> | ||
| + | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 19:50 5 jul 2007
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Ecuación de primer grado con dos incógnitas
Una ecuación de primer grado con dos incógnitas es aquella que se puede expresar de la forma:
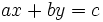
donde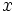 
e 
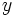son variables 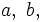y 
y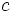 
constantes.
Ejemplo: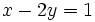 
Soluciones de una ecuación de primer grado con dos incógnitas
Una ecuación de primer grado con dos incógnitas tiene infinitas soluciones. Para cada valor que le asignemos a la variable 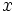, podemos encontrar un valor de la variable 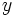despejándola en la ecuación.
Ejemplo: Ecuación de primer grado con dos incógnitas
- Halla algunas soluciones para la ecuación:
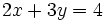
Despejamos la variable y:
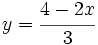
Construimos una tabla de valores, dandole valores a 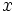y calculando 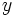en la expresión anterior:
| x | -1 | 2 | 5 | ... |
| y | 2 | 0 | -2 | ... |
Las soluciones vienen dadas por las parejas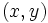 
así obtenidas:
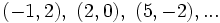
Compruébalas en la siguiente escena:
Sistemas de ecuaciones 2x2
Un sistema de dos ecuaciones de primer grado con dos incógnitas o simplemente, sistema 2x2, es la agrupación de dos ecuaciones de primer grado con dos incógnitas:
