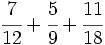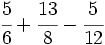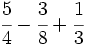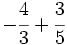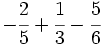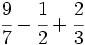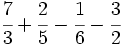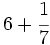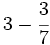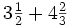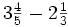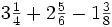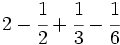Fracciones: Suma y resta (1º ESO)
De Wikipedia
| Revisión de 16:38 25 sep 2016 Coordinador (Discusión | contribuciones) (→Suma y resta de fracciones con el mismo denominador) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Suma y resta de fracciones con distinto denominador) |
||
| Línea 9: | Línea 9: | ||
| (Pág. 138) | (Pág. 138) | ||
| {{p}} | {{p}} | ||
| + | ==Suma y resta de fracciones== | ||
| + | En el siguiente videotutorial se condensa todo lo visto en este tema sobre suma y resta de fracciones: | ||
| + | |||
| + | {{Video: Suma y resta de fracciones}} | ||
| + | {{p}} | ||
| + | |||
| ==Suma y resta de fracciones con el mismo denominador== | ==Suma y resta de fracciones con el mismo denominador== | ||
| - | {{Tabla75|celda2=[[Imagen:suma_frac_mismo_den.jpg|thumb|Fig.1: Suma de fracciones con el mismo denominador]] | + | {{Tabla75|celda2=[[Imagen:suma_frac_mismo_den.jpg|thumb|250px|Fig.1: Suma de fracciones con el mismo denominador]] |
| |celda1= | |celda1= | ||
| - | {{Teorema_sin_demo|titulo=Procedimiento|enunciado=Para sumar o restar fracciones con el mismo denominador, sumamos o restamos los numeradores y dejamos el mismo denominador}} | + | {{Teorema_sin_demo|titulo=Procedimiento: ''Suma de fracciones con el mismo denominador''|enunciado=Para sumar o restar fracciones con el mismo denominador, sumamos o restamos los numeradores y dejamos el mismo denominador |
| + | }} | ||
| {{p}} | {{p}} | ||
| - | {{Ejemplo_simple|titulo=Ejemplos|contenido= | + | {{Warning|titulo=Advertencia:|texto=Cuando hagamos operaciones con fracciones, no sólo la suma y la resta, es posible que el resultado sea una fracción que se pueda simplificar. Es importante que te acostumbres a simplificar el resultado todo lo que sea posible. En la Fig.1, por ejemplo, el resultado que deberíamos dar es 3/4 en lugar de 6/8. |
| - | *<math>\cfrac{2}{8}+\cfrac{4}{8}=\cfrac{4+2}{8} = \cfrac{6}{8}</math> | + | }} |
| + | }} | ||
| + | {{p}} | ||
| + | {{Ejemplo|titulo=Ejemplos: ''Suma y resta de fracciones con el mismo denominador''|enunciado= | ||
| + | Calcula: | ||
| + | |||
| + | :a) <math>\cfrac{2}{8}+\cfrac{4}{8}</math>{{b4}}{{b4}} b) <math>\cfrac{5}{7}-\cfrac{3}{7}</math> | ||
| + | |||
| + | |sol= | ||
| + | a) <math>\cfrac{2}{8}+\cfrac{4}{8}=\cfrac{4+2}{8} = \cfrac{6}{8}</math> | ||
| + | |||
| {{b4}} | {{b4}} | ||
| - | *<math>\cfrac{5}{7}-\cfrac{3}{7}=\cfrac{5-3}{7} =\cfrac{2}{7} </math> | + | |
| + | b) <math>\cfrac{5}{7}-\cfrac{3}{7}=\cfrac{5-3}{7} =\cfrac{2}{7} </math> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Videotutoriales suma y resta fracciones con mismo denominador}} | ||
| + | {{Actividades|titulo=Suma y resta de fracciones con el mismo denominador|enunciado= | ||
| + | {{AI_anaya | ||
| + | |titulo1=Actividad | ||
| + | |descripcion=Suma y resta de fracciones con mismo denominador. | ||
| + | |url1=http://www.joaquincarrion.com/Recursosdidacticos/QUINTO/datos/03_Mates/datos/05_rdi/ud07/2/02.htm | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 1 (suma) | ||
| + | |descripcion=Suma de fracciones con el mismo denominador. | ||
| + | |url1=http://es.khanacademy.org/math/arithmetic/fraction-arithmetic/arith-review-adding-subtracting-frac/e/adding_fractions_with_common_denominators | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 2 (resta) | ||
| + | |descripcion=Resta de fracciones con el mismo denominador. | ||
| + | |url1=http://es.khanacademy.org/math/arithmetic/fraction-arithmetic/arith-review-adding-subtracting-frac/e/subtracting_fractions_with_common_denominators | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 3 (números mixtos) | ||
| + | |descripcion=Suma y resta números mixtos. | ||
| + | |url1=http://es.khanacademy.org/math/arithmetic/fraction-arithmetic/arith-review-adding-subtracting-frac/e/adding_subtracting_mixed_numbers_0.5 | ||
| }} | }} | ||
| }} | }} | ||
| Línea 23: | Línea 64: | ||
| ==Suma y resta de fracciones con distinto denominador== | ==Suma y resta de fracciones con distinto denominador== | ||
| - | {{AI_enlace | + | {{Tabla75|celda2=[[Imagen:suma_frac_dist_den.gif|thumb|250px|Fig.2: Suma de fracciones con distinto denominador]] |
| - | |titulo1=Actividades: ''Suma y resta de fracciones'' | + | |celda1= |
| - | |descripcion= | + | {{Teorema_sin_demo|titulo=Procedimiento: ''Suma de fracciones con distinto denominador''|enunciado=Para sumar o restar fracciones con distinto denominador, primero se reducen las fracciones a común denominador y luego se procede como en el caso en el que las fracciones tienen el mismo denominador.}} |
| - | <center><iframe>url=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/08/03.htm | + | {{p}} |
| - | width=850 | + | {{Nota|titulo=Observación:|texto=#Si en una suma de fracciones alguno de los sumandos es un número entero, se le considerará como si fuera una fracción con denominador unidad. |
| - | height=650 | + | #Una vez hemos reducido a denominador común, las sumas y restas con los numeradores no dejan de ser sumas y restas con números enteros, así que las reglas para esas operaciones se conservan (paréntesis, orden de las operaciones, ...). Haremos hicapié en esto cuando veamos las [[Fracciones: Operaciones combinadas (1º ESO)|operaciones combinadas con fracciones]].}} |
| - | name=myframe | + | {{p}} |
| - | </iframe></center> | + | {{Ejemplo|titulo=Ejemplos: ''Suma y resta de fracciones con distinto denominador''|enunciado= |
| - | |url1=http://maralboran.org/web_ma/Anaya/Anaya07/1ESO_ALUMNO/datos/08/03.htm | + | :a) <math>\cfrac{1}{5}+\cfrac{1}{2}</math>{{b4}}{{b4}} b) <math>2-\cfrac{5}{6}+\cfrac{3}{4}</math> |
| + | |sol= | ||
| + | a) m.c.m.(5, 2) = 10 | ||
| + | |||
| + | <center><math>\cfrac{1}{5}+\cfrac{1}{2} \ = \ \cfrac{2}{10} + \cfrac{5}{10} \ = \ \cfrac{7}{10}</math> {{b4}}(Ver Fig. 2)</center> | ||
| + | |||
| + | {{b4}} | ||
| + | |||
| + | b) m.c.m.(1 ,6, 4) = 12 | ||
| + | |||
| + | <center><math>2-\cfrac{5}{6}+\cfrac{3}{4} \ = \ \cfrac{2}{1}-\cfrac{5}{6}+\cfrac{3}{4} \ = \ \cfrac{24}{12}-\cfrac{10}{12}+\cfrac{9}{12} \ = \ \cfrac{24-10+9}{12} =\cfrac{23}{12}</math></center> | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Videotutoriales suma y resta fracciones con distinto denominador}} | ||
| + | {{Actividades|titulo=Suma y resta de fracciones con distinto denominador|enunciado= | ||
| + | {{AI_anaya | ||
| + | |titulo1=Actividad 1 | ||
| + | |descripcion=Atividades para aprender a sumar fracciones con distinto denominador. | ||
| + | |url1=http://www.iespravia.com/carpetas/recursos/mates/anaya1/datos/08/01.htm | ||
| + | }} | ||
| + | {{AI_anaya | ||
| + | |titulo1=Actividad 2 | ||
| + | |descripcion=Suma y resta de fracciones con distinto denominador. | ||
| + | |url1=http://www.joaquincarrion.com/Recursosdidacticos/SEXTO/datos/03_Mates/datos/05_rdi/ud08/2/02.htm | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 1 (suma y resta: método gráfico) | ||
| + | |descripcion=Suma y resta visual de fracciones. | ||
| + | |url1=http://es.khanacademy.org/math/arithmetic/fraction-arithmetic/arith-review-add-sub-fractions/e/using-visuals-to-add-and-subtract-fractions-with-unlike-denominators- | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 2 (suma: m.c.m.) | ||
| + | |descripcion=Suma de fracciones con distinto denominador. | ||
| + | |url1=http://es.khanacademy.org/math/arithmetic/fraction-arithmetic/arith-review-add-sub-fractions/e/adding_fractions | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 3 (resta: m.c.m.) | ||
| + | |descripcion=Resta de fracciones con distinto denominador. | ||
| + | |url1=http://es.khanacademy.org/math/arithmetic/fraction-arithmetic/arith-review-add-sub-fractions/e/subtracting_fractions | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 4 (números mixtos I) | ||
| + | |descripcion=Suma y resta de números mixtos (nivel I). | ||
| + | |url1=http://es.khanacademy.org/math/arithmetic/fraction-arithmetic/arith-review-add-sub-mix-num-w-unlike-den/e/adding_subtracting_mixed_numbers_1 | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 5 (números mixtos II) | ||
| + | |descripcion=Suma y resta de números mixtos (nivel II). | ||
| + | |url1=http://es.khanacademy.org/math/arithmetic/fraction-arithmetic/arith-review-add-sub-mix-num-w-unlike-den/e/adding-and-subtracting-mixed-numbers-with-unlike-denominators-2 | ||
| + | }} | ||
| + | }} | ||
| + | |||
| + | ==Actividades== | ||
| + | {{Videotutoriales|titulo=Problemas|enunciado= | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Problema 1 | ||
| + | |duracion=5'17" | ||
| + | |sinopsis=Pedro tiene que practicar piano 3/4 de hora diariamente. Si el día de hoy lleva 1/4 de hora. ¿Qué fracción de hora le falta por practicar? | ||
| + | |url1=https://www.youtube.com/watch?v=HXcWEj0shkM | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Problema 2 | ||
| + | |duracion=3'57" | ||
| + | |sinopsis=Antonio y Bernardo atraparon un lagarto en su patio trasero. Si el cuerpo del lagarto mide 17/8 dm y su cola mide 10/8 dm. ¿Cuánto miden juntos el cuerpo y la cola del lagarto? | ||
| + | |url1=https://www.youtube.com/watch?v=otZ5hNkniRE | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Problema 3 | ||
| + | |duracion=8'48" | ||
| + | |sinopsis=Camila y Ernesto necesitan 1 litro de pintura anaranjada para terminar la piñata gigante que están haciendo para las festividades de la escuela. Camila tiene 2/3 de litro de pintura roja y Ernesto tiene 1/2 litro de pintura amarilla. Si deciden mezclar sus pinturas para formar pintura anaranjada, ¿tienen suficiente pintura para terminar la piñata? | ||
| + | |url1=https://www.youtube.com/watch?v=b3S3Q_-bDKQ | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Problema 4 | ||
| + | |duracion=5'28" | ||
| + | |sinopsis=Elena está cultivando plantas de tomate y estudiando sus alturas, obteniendo los siguientes resultados (en números mixtos): | ||
| + | |||
| + | Tipo de tomate Altura (pies) | ||
| + | -------------- ------------- | ||
| + | Bola 3 1/4 | ||
| + | Roma 2 7/8 | ||
| + | Cereza 3 1/2 | ||
| + | |||
| + | ¿Cuál es la diferencia entre las alturas de las plantas de tomate tipo Bola y tipo Roma? | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=e_7kEHJgTpI | ||
| + | }} | ||
| + | }} | ||
| + | {{actividades suma y resta fracciones 1ºESO}} | ||
| + | {{p}} | ||
| + | {{wolfram suma y resta fracciones}} | ||
| + | |||
| ==Ejercicios propuestos== | ==Ejercicios propuestos== | ||
| {{ejercicio | {{ejercicio | ||
| Línea 40: | Línea 171: | ||
| (Pág. 139) | (Pág. 139) | ||
| - | [[Imagen:red_star.png|12px]] | + | [[Imagen:red_star.png|12px]] 2a,b,c,d; 5a,d; 6a,e,f; 8; 9; 10; 11 |
| - | [[Imagen:yellow_star.png|12px]] | + | [[Imagen:yellow_star.png|12px]] 1; 2e,f,g,h,i,j; 3; 4; 5b,c; 6b,c,d,g,h; 7; |
| |sol= | |sol= | ||
Revisión actual
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 138)
Suma y resta de fracciones
En el siguiente videotutorial se condensa todo lo visto en este tema sobre suma y resta de fracciones:
- Suma y resta de fracciones con el mismo denominador.
- Suma y resta de fracciones con el distinto denominador.
- Ejemplos.
Suma y resta de fracciones con el mismo denominador
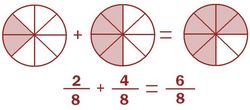
Procedimiento: Suma de fracciones con el mismo denominador Para sumar o restar fracciones con el mismo denominador, sumamos o restamos los numeradores y dejamos el mismo denominador Cuando hagamos operaciones con fracciones, no sólo la suma y la resta, es posible que el resultado sea una fracción que se pueda simplificar. Es importante que te acostumbres a simplificar el resultado todo lo que sea posible. En la Fig.1, por ejemplo, el resultado que deberíamos dar es 3/4 en lugar de 6/8. |
Suma de fracciones con el mismo denominador. Lo que en este video se explica es válido para la resta sin más que cambiar suma por resta.
Suma de fracciones con el mismo denominador.
Resta de fracciones con el mismo denominador.
Suma de fracciones mixtas con el mismo denominador.
Resta de fracciones mixtas con el mismo denominador.
Suma y resta de fracciones con el mismo denominador:
a) 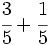 b)
b) 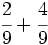 c)
c) 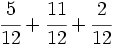 d)
d) 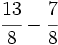 e)
e) 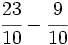
Suma y resta de fracciones con el mismo denominador.
Suma y resta de fracciones con mismo denominador.
Suma de fracciones con el mismo denominador.
Resta de fracciones con el mismo denominador.
Suma y resta números mixtos.
Suma y resta de fracciones con distinto denominador
Procedimiento: Suma de fracciones con distinto denominador Para sumar o restar fracciones con distinto denominador, primero se reducen las fracciones a común denominador y luego se procede como en el caso en el que las fracciones tienen el mismo denominador.
|
Suma de fracciones usando el método gráfico.
Resta de fracciones usando el método gráfico.
Suma de fracciones usando el método del m.c.m.
Resta de fracciones usando el método del m.c.m.
Suma de números mixtos usando el método del m.c.m.
Resta de números mixtos usando el método del m.c.m.
Suma y resta de fracciones usando el método del m.c.m.
Otro método para sumar o restar fracciones, fácil de recordar, que no requiere del m.c.m, pero que a veces precisa simplificar más al final. Lo que en este video se explica es válido para la resta sin más que cambiar suma por resta.
Suma y resta de fracciones con distinto denominador (método rápido) Suma y resta de fracciones con distinto denominador (método del m.c.m.): a) Suma de fracciones con distinto denominador (método rápido): a) b) Resta de fracciones con distinto denominador (método rápido): a) b) Suma de fracciones con distinto denominador (método del m.c.m.): a) Suma y resta de fracciones con distinto denominador (método del m.c.m.): Suma y resta de fracciones con distinto denominador (método del m.c.m.): Suma y resta de fracciones con distinto denominador:
Suma y resta de fracciones con distinto denominador (método rápido): | Suma y resta de cuatro fracciones con distinto denominador(método del m.c.m.): Suma de un entero y una fracción: Resta de un entero y una fracción. Suma de números mixtos. Resta de números mixtos. Suma y resta de números mixtos. Calcula: Calcula: |
Si Fernando recoge 3/4 de kilo de verdura y David recoge 1/8 de kilo de verdura, calcula los kilos de verdura que han recogido entre los dos e indica aquél que ha recogido menos cantidad.
Atividades para aprender a sumar fracciones con distinto denominador.
Suma y resta de fracciones con distinto denominador.
Suma y resta visual de fracciones.
Suma de fracciones con distinto denominador.
Resta de fracciones con distinto denominador.
Suma y resta de números mixtos (nivel I).
Suma y resta de números mixtos (nivel II).
Actividades
Pedro tiene que practicar piano 3/4 de hora diariamente. Si el día de hoy lleva 1/4 de hora. ¿Qué fracción de hora le falta por practicar?
Antonio y Bernardo atraparon un lagarto en su patio trasero. Si el cuerpo del lagarto mide 17/8 dm y su cola mide 10/8 dm. ¿Cuánto miden juntos el cuerpo y la cola del lagarto?
Camila y Ernesto necesitan 1 litro de pintura anaranjada para terminar la piñata gigante que están haciendo para las festividades de la escuela. Camila tiene 2/3 de litro de pintura roja y Ernesto tiene 1/2 litro de pintura amarilla. Si deciden mezclar sus pinturas para formar pintura anaranjada, ¿tienen suficiente pintura para terminar la piñata?
Elena está cultivando plantas de tomate y estudiando sus alturas, obteniendo los siguientes resultados (en números mixtos):
Tipo de tomate Altura (pies)
-------------- -------------
Bola 3 1/4
Roma 2 7/8
Cereza 3 1/2
¿Cuál es la diferencia entre las alturas de las plantas de tomate tipo Bola y tipo Roma?
Actividades en las que aprenderás y practicarás la suma de fracciones por el método del m.c.m.
Actividades en las que aprenderás y practicarás la suma y resta de fracciones por el método del m.c.m.
Suma de fracciones.
Resta de fracciones.
Suma y resta de fracciones.
Suma y resta de fracciones.
Problemas de sumas y restas de fracciones con los mismos denominadores.
Problemas de sumas y restas de fracciones con distintos denominadores.
Ejercicios propuestos
|
Ejercicios propuestos: Suma y resta de fracciones |
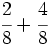 b)
b) 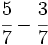
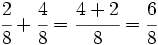
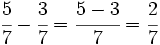
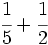 b)
b) 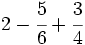
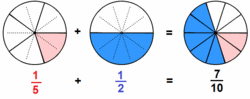
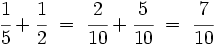 (Ver Fig. 2)
(Ver Fig. 2)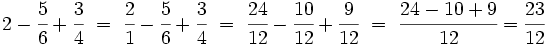
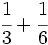 b)
b) 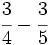
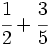
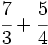
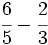
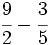
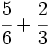 b)
b) 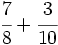 c)
c)