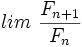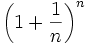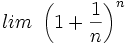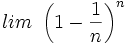Algunos límites importantes (1ºBach)
De Wikipedia
| Revisión de 11:55 18 sep 2016 Coordinador (Discusión | contribuciones) (→El número ''e'') ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→El número ''e'') |
||
| Línea 57: | Línea 57: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Video_enlace | + | {{Video_enlace_clasematicas |
| - | |titulo1=Un número llamado e | + | |titulo1=Límites del número e |
| - | |duracion=13' | + | |duracion=34´22" |
| - | |url1=http://www.rtve.es/alacarta/videos/mas-por-menos/aventura-del-saber-serie-mas-menos-numero-llamado/1296636/ | + | |url1=https://www.youtube.com/watch?v=TKkSMKfUBA0&index=8&list=PLZNmE9BEzVIkITepuGQcKXJ-FuD5p7cP5 |
| - | |titulo2=Acceso por red TIC | + | |sinopsis=Tutorial en el que se explica y trabajan los límites que generan al número e. Mediante una primera explicación algo teórica y muchos ejemplos, se da a conocer este tipo de límites y los pasos a seguir para su cálculo, evitando la indeterminación de 1 elevado a infinito |
| - | |url2=http://c0/helvia/aula/archivos/repositorio//0/90/html/index.htm | + | }} |
| - | |titulo3=acceso por maralboran.org | + | {{Videotutoriales|titulo=El número e|enunciado= |
| - | |url3=http://maralboran.org/web_ma/videos/elnumeroe/elnumeroe.htm | + | {{Video: Que es el numero e}} |
| - | |sinopsis=Hay números que nos sorprenden por su tendencia a aparecer en las situaciones más inesperadas. ¿ Qué pueden tener en común los cables del tendido eléctrico, las cuentas bancarias, el desarrollo de una colonia de bacterias, la prueba del carbono 14 para datar restos orgánicos, las encuestas de población, la probabilidad de sacar 70 veces un número par al lanzar un dado 100 veces...? Aparentemente nada. Sin embargo en todas estas situaciones interviene un extraño número comprendido entre 2 y 3, que tiene infinitas cifras decimales y un origen un tanto exótico. Al igual que el más famoso número pi, los matemáticos le conocen mediante una letra. Es un número llamado e. | + | {{Video: Un numero llamado e}} |
| }} | }} | ||
| - | |||
| (Pág. 65) | (Pág. 65) | ||
| Línea 105: | Línea 104: | ||
| {{Teorema | {{Teorema | ||
| |titulo= Límite de la suma de n primeros términos de una progresión geométrica | |titulo= Límite de la suma de n primeros términos de una progresión geométrica | ||
| - | |enunciado=:Sea <math>a_n\;</math> una progresión geométrica de razón <math>r\;</math> y sea <math>S_n=\frac{a_1 r^n-a_1}{r-1}</math> la suma de sus n primeros términos | + | |enunciado=Sea <math>a_n\;</math> una progresión geométrica de razón <math>r\;</math> y sea <math>S_n=\frac{a_1 r^n-a_1}{r-1}</math> la suma de sus n primeros términos |
| - | ::* Si <math> 0<\; \mid r \mid \; <1 </math>, entonces el límite de <math>S_n\;</math> existe y su valor es: | + | :* Si <math> 0<\; \mid r \mid \; <1 </math>, entonces el límite de <math>S_n\;</math> existe y su valor es: |
| <center><math>S_{\infty}=lim \ S_n = \frac{a_1}{1-r}</math></center> | <center><math>S_{\infty}=lim \ S_n = \frac{a_1}{1-r}</math></center> | ||
| - | ::*Si <math>r\ge 1\;</math>, entonces el límite de <math>S_n\;</math> es <math>+\infty \;</math> o <math>-\infty</math>: | + | :*Si <math>r\ge 1\;</math>, entonces el límite de <math>S_n\;</math> es <math>+\infty \;</math> o <math>-\infty</math>: |
| <center><math>S_{\infty}=lim \ S_n =\begin{cases} +\infty, & \mbox{si }a_1>0\mbox{ } \\ -\infty, & \mbox{si }a_1<0\mbox{ } \end{cases}</math></center> | <center><math>S_{\infty}=lim \ S_n =\begin{cases} +\infty, & \mbox{si }a_1>0\mbox{ } \\ -\infty, & \mbox{si }a_1<0\mbox{ } \end{cases}</math></center> | ||
| - | ::*Si <math>r\le -1\;</math>, entonces el límite de <math>S_n\;</math> no existe. | + | :*Si <math>r\le -1\;</math>, entonces el límite de <math>S_n\;</math> no existe. |
| Línea 160: | Línea 159: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Actividades== | ==Actividades== | ||
| {{wolfram desplegable|titulo=Algunos límites importantes|contenido= | {{wolfram desplegable|titulo=Algunos límites importantes|contenido= | ||
| Línea 168: | Línea 168: | ||
| |enunciado= | |enunciado= | ||
| - | :'''1.''' Dada la sucesión de Fibonacci <math>F_n \;</math> | + | '''1.''' Dada la sucesión de Fibonacci <math>F_n \;</math> |
| - | ::a) Calcula sus 10 primeros términos. | + | |
| - | ::b) Calcula los 10 primeros términos de <math>\frac{F_{n+1}}{F_{n}}</math>. | + | :a) Calcula sus 10 primeros términos. |
| - | ::c) Calcula <math>lim \ \frac{F_{n+1}}{F_{n}}</math> | + | |
| + | :b) Calcula los 10 primeros términos de <math>\frac{F_{n+1}}{F_{n}}</math>. | ||
| + | |||
| + | :c) Calcula <math>lim \ \frac{F_{n+1}}{F_{n}}</math> | ||
| {{p}} | {{p}} | ||
| - | :'''2.''' Dada la sucesión <math>\left ( 1 + \frac{1}{n} \right )^n</math> | + | '''2.''' Dada la sucesión <math>\left ( 1 + \frac{1}{n} \right )^n</math> |
| - | ::a) Calcula sus 10 primeros términos. | + | |
| - | ::b) Calcula <math>lim \ \left ( 1 + \frac{1}{n} \right )^n</math> | + | :a) Calcula sus 10 primeros términos. |
| - | {{p}} | + | |
| - | :'''3.''' Calcula <math>lim \ \left ( 1 - \frac{1}{n} \right )^n</math> | + | :b) Calcula <math>lim \ \left ( 1 + \frac{1}{n} \right )^n</math> |
| + | |||
| + | '''3.''' Calcula <math>lim \ \left ( 1 - \frac{1}{n} \right )^n</math> | ||
| {{p}} | {{p}} | ||
| |sol= | |sol= | ||
| Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| - | :1. | + | 1. |
| - | ::a) {{consulta|texto=Table[Fibonacci[n],{n,1,10}]}} | + | :a) {{consulta|texto=Table[Fibonacci[n],{n,1,10}]}} |
| - | ::b) {{consulta|texto=Table[Fibonacci[n+1]/Fibonacci[n],{n,1.,10.}]}} | + | :b) {{consulta|texto=Table[Fibonacci[n+1]/Fibonacci[n],{n,1.,10.}]}} |
| - | ::c) {{consulta|texto= limit Fibonacci[n+1]/Fibonacci[n] as n->+oo}} | + | :c) {{consulta|texto= limit Fibonacci[n+1]/Fibonacci[n] as n->+oo}} |
| - | :2. | + | 2. |
| - | ::a) {{consulta|texto=Table[(1+1/n)^n,{n,1.,10.}]}} | + | :a) {{consulta|texto=Table[(1+1/n)^n,{n,1.,10.}]}} |
| - | ::b) {{consulta|texto= limit (1+1/n)^n as n->+oo}} | + | :b) {{consulta|texto= limit (1+1/n)^n as n->+oo}} |
| - | :3. | + | 3. |
| - | :: {{consulta|texto= limit (1-1/n)^n as n->+oo}} | + | : {{consulta|texto= limit (1-1/n)^n as n->+oo}} |
| {{widget generico}} | {{widget generico}} | ||
| }} | }} | ||
| Línea 199: | Línea 204: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | |||
| ==Ejercicios propuestos== | ==Ejercicios propuestos== | ||
| {{ejercicio | {{ejercicio | ||
| |titulo=Ejercicios propuestos: ''Algunos límites importantes'' | |titulo=Ejercicios propuestos: ''Algunos límites importantes'' | ||
| |cuerpo= | |cuerpo= | ||
| - | :(Pág. 65) | + | (Pág. 65) |
| - | :[[Imagen:yellow_star.png|12px]] 2, 3 | + | [[Imagen:yellow_star.png|12px]] 2, 3 |
| }} | }} | ||
| {{p}} | {{p}} | ||
| [[Categoría: Matemáticas]][[Categoría: Números]] | [[Categoría: Matemáticas]][[Categoría: Números]] | ||
Revisión actual
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | Número e Número áureo | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
(Pág. 64)
El número e
La sucesión del número e El número 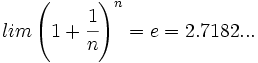 Demostración: La demostración excede el nivel de este curso. Ver demostración. Otra sucesión del número e Dada la sucesión: 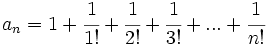 se cumple que: 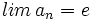 Demostración: Demostraremos sólo que esta sucesión tiene límite. Demostrar que el límite es el número Para la demostración usaremos el teorema dice que "Toda sucesión de números reales monótona y acotada es convergente". En este caso, nuetra sucesión es monotona creciente y acotada superiormente. Veámoslo:
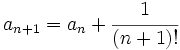
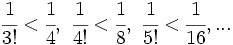
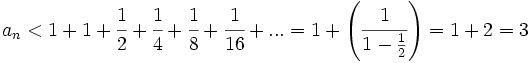
|  Leonard Euler El número e, base de los logaritmos neperianos, lleva este nombre en su honor (inicial de su apellido) |
Tutorial en el que se explica y trabajan los límites que generan al número e. Mediante una primera explicación algo teórica y muchos ejemplos, se da a conocer este tipo de límites y los pasos a seguir para su cálculo, evitando la indeterminación de 1 elevado a infinito
¿Qué tiene el número Pi que no tenga e?
Te explicamos uno de los más importantes números reales irracionales y trascendentes, base de los logaritmos neperianos.
Hay números que nos sorprenden por su tendencia a aparecer en las situaciones más inesperadas. ¿ Qué pueden tener en común los cables del tendido eléctrico, las cuentas bancarias, el desarrollo de una colonia de bacterias, la prueba del carbono 14 para datar restos orgánicos, las encuestas de población, la probabilidad de sacar 70 veces un número par al lanzar un dado 100 veces...? Aparentemente nada. Sin embargo en todas estas situaciones interviene un extraño número comprendido entre 2 y 3, que tiene infinitas cifras decimales y un origen un tanto exótico. Al igual que el más famoso número pi, los matemáticos le conocen mediante una letra. Es un número llamado e.
(Pág. 65)
El número áureo, 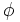
La sucesión de Fibonacci y el número áureo
Si a partir de la sucesión de Fibonacci
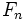 = 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,...,
= 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,...,construimos, por recurrencia, la sucesión
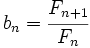
Entonces, esta sucesión tiende al número áureo:
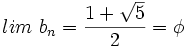
Comprobación: Si en la sucesión de Fibonacci
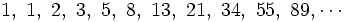
dividimos cada término entre el anterior, tenemos:
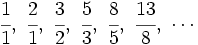
que expresada con decimales nos da:
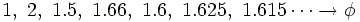
Demostración:
Por construcción de la sucesión de Fibonacci:
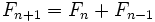
Dividiendo ambos miembros por 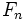 :
:
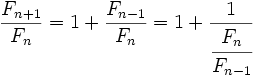
Tomando límites en ambos miembros:
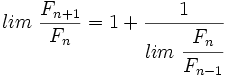
Llamando 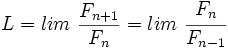 , tenemos:
, tenemos:
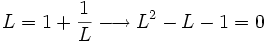
ecuación de segundo grado cuya única raíz válida es:
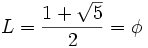
Documental sobre el número aureo.
El programa presenta a este exótico número ya conocido por los griegos. Veremos cómo se obtiene, qué son los rectángulos áureos y su presencia en infinidad de manifestaciones artísticas, en Pintura, Arquitectura, Escultura... a lo largo de la historia. Pero el número de oro no es un mero invento del hombre, la naturaleza nos sorprende de una forma que no puede ser casual, tanto en el mundo vegetal como en el animal, como en multitud de fenómenos físicos, con acontecimientos en los que este famosos número hace acto de presencia.
A lo largo de la historia, Phi, el número de oro o número áureo, ha representado, para las personas que lo han conocido, la belleza, la magia, la perfección, lo divino. ¿Por qué?. Página elaborada por D. Luis Nicolás Ortiz.
Suma de los términos de una progresión geométrica
Límite de la suma de n primeros términos de una progresión geométrica
Sea 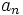 una progresión geométrica de razón
una progresión geométrica de razón 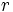 y sea
y sea 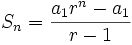 la suma de sus n primeros términos
la suma de sus n primeros términos
- Si
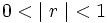 , entonces el límite de
, entonces el límite de 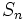 existe y su valor es:
existe y su valor es:
- Si
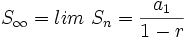
- Si
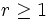 , entonces el límite de
, entonces el límite de 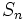 es
es 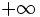 o
o 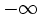 :
:
- Si
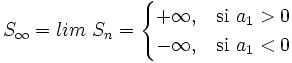
- Si
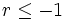 , entonces el límite de
, entonces el límite de 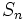 no existe.
no existe.
- Si
- Si
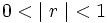 , entonces
, entonces
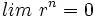 y
y 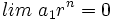 .
.(Por ejemplo, si a1 = 3 y r = 0.5, al multiplicar sucesivas veces 3 por 0.5, lo que equivale a dividir por 2, el resultado se aproxima cada vez más a cero.)
y por tanto
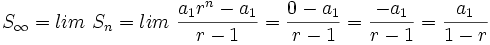
- Si
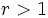 , entonces
, entonces
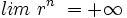 y
y 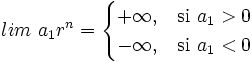
(Por ejemplo, si a1 = 3 y r = 5, al multiplicar sucesivas veces 3 por 5, el resultado se aproxima cada vez más a 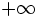 . Mientras que si a1 = − 3 y r = 5, al multiplicar sucesivas veces -3 por 5, el resultado se aproxima cada vez más a
. Mientras que si a1 = − 3 y r = 5, al multiplicar sucesivas veces -3 por 5, el resultado se aproxima cada vez más a 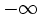 )
)
y por tanto
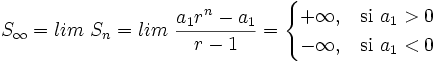
- Si
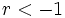 , entonces
, entonces 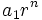 va alternando valores positivos y negativos, cada vez mayores en valor absoluto, de manera que a la sucesión
va alternando valores positivos y negativos, cada vez mayores en valor absoluto, de manera que a la sucesión 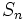 también va a oscilar en signo y no tiene límite.
también va a oscilar en signo y no tiene límite.
- Si
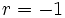 , el caso es muy sencillo, porque la progresión quedaría:
, el caso es muy sencillo, porque la progresión quedaría:
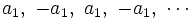
y la sucesión 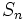 sería:
sería:
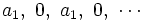
que oscila y no tiene límite.
- Si
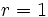 , la progresión quedaría constante:
, la progresión quedaría constante:
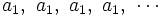 , .
, .y tendríamos que 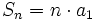 , cuyo límite es:
, cuyo límite es:
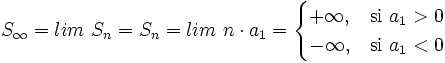
Actividades
|
Actividad: Algunos límites importantes 1. Dada la sucesión de Fibonacci
2. Dada la sucesión
3. Calcula Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: 1.
2.
|
Ejercicios propuestos
|
Ejercicios propuestos: Algunos límites importantes |
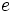 , se define como el límite de una sucesión:
, se define como el límite de una sucesión:
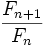 .
.