Plantilla:Raíces de un polinomio
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:23 29 oct 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | {{Caja_Amarilla|texto=Un número <math>a\,</math> es una '''raíz''' o un '''cero''' de un polinomio <math>P(x)\,</math>, si <math>P(a)\, = 0\,</math>. Dicho de otra forma, las raíces de un polinomio son las soluciones de la ecuación <math>P(x)\,= 0\,</math>.}} | + | {{Caja_Amarilla|texto=Un número <math>a\,</math> es una '''raíz''' o un '''cero''' de un polinomio <math>P(x)\,</math>, si <math>P(a)\, = 0\,</math>. |
| + | |||
| + | Dicho de otra forma, las raíces de un polinomio son las soluciones de la ecuación <math>P(x)\,= 0\,</math>.}} | ||
| + | {{p}} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Raíces de un polinomio | ||
| + | |duracion=8'40" | ||
| + | |sinopsis=Raíces de un polinomio. Ejemplos. | ||
| + | |url1=https://youtu.be/MMnsY36Dtlk?list=PLwCiNw1sXMSDgbsuqToHr0F45-YoSUP7d | ||
| + | }} | ||
| {{p}} | {{p}} | ||
| {{teorema|titulo=Teorema del factor | {{teorema|titulo=Teorema del factor | ||
| |enunciado=<math>x=a\;</math> es una raíz de un polinomio <math>P(x)\;</math> si y solo si <math>(x-a)\;</math> es un factor de dicho polinomio. | |enunciado=<math>x=a\;</math> es una raíz de un polinomio <math>P(x)\;</math> si y solo si <math>(x-a)\;</math> es un factor de dicho polinomio. | ||
| |demo= | |demo= | ||
| - | Es una consecuencia directa del [[Factorización de Polinomios (4ºESO-B)#Teorema del resto|teorema del resto]]. En efecto, si <math>x=a\;</math> es una raíz de <math>P(x)\;</math>, entonces <math>P(a)=0\;</math> y, por el teorema del resto, el resto de dividir <math>P(x)\;</math> entre <math>(x-a)\;</math> es cero. Así <math>(x-a)\;</math> es un factor de <math>P(x)\;</math>. El recíproco es trivial. | + | En efecto, si <math>x=a\;</math> es una raíz de <math>P(x)\;</math>, entonces <math>P(a)=0\;</math> y, por el [[Regla de Ruffini (4ºESO Académicas)#Teorema del resto|teorema del resto]], el resto de dividir <math>P(x)\;</math> entre <math>(x-a)\;</math> es cero. Así <math>(x-a)\;</math> es un factor de <math>P(x)\;</math>. |
| + | |||
| + | El recíproco es trivial. | ||
| }} | }} | ||
Revisión actual
Un número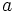 
es una raíz o un cero de un polinomio 
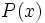, si 
.
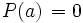Dicho de otra forma, las raíces de un polinomio son las soluciones de la ecuación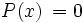 
.
Raíces de un polinomio (8'40") Sinopsis:Raíces de un polinomio. Ejemplos.
Teorema del factor
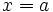es una raíz de un polinomio 
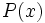si y solo si 
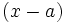es un factor de dicho polinomio.
Demostración:
En efecto, si 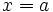es una raíz de 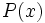, entonces 
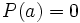y, por el teorema del resto, el resto de dividir 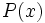entre 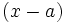es cero. Así 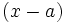es un factor de .
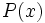