Plantilla:Discriminante de la ecuación de segundo grado

De Wikipedia

(Diferencia entre revisiones)

Saltar a navegación, búsqueda

Revisión actual

Llamamos discriminante de una ecuación de segundo grado, 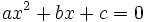$ax^2+bx+c=0 \;$ , al número:

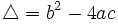
$\triangle = b^2-4ac$

Proposición

Sea $\triangle$ el discriminante de una ecuación de segundo grado:

Si 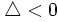$\triangle <0$ , la ecuación no tiene solución.
Si 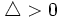$\triangle >0$ , la ecuación tiene dos soluciones.
Si 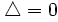$\triangle =0$ , la ecuación tiene una solución (doble).

Demostración:

La demostración es inmediata teniendo en cuenta la fórmula para la resolución de la ecuación de segundo grado:

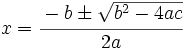
$x=\cfrac{-b \pm \sqrt {b^2-4ac}}{2a}$

ya que, lo que hay en el radicando, es precisamente el discriminante. Por tanto,

Si su signo es positivo, la raíz existe y da lugar a dos soluciones distintas.
Si su signo es negativo, la raíz no existe y no hay ninguna solución.
Si es cero, la raíz vale cero, y hay dos soluciones iguales (solución doble).

Discriminante y número de soluciones

Tutorial (5'42") Sinopsis:

Número de soluciones de una ecuación de 2º grado. Discriminante.

Ejercicio 1 (3'04") Sinopsis:

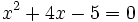Halla el discriminante para determinar el número de raíces de la ecuación $x^2+4x-5=0\;$ .

Ejercicio 2 (3'17") Sinopsis:

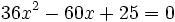Halla el discriminante para determinar el número de raíces de la ecuación $36x^2-60x+25=0\;$ .

Ejercicio 3 (3'29") Sinopsis:

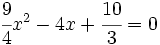Halla el discriminante para determinar el número de raíces de la ecuación $\cfrac{9}{4}x^2-4x+\cfrac{10}{3}=0\;$ .

Ejercicio 4 (3'42") Sinopsis:

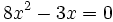Halla el discriminante para determinar el número de raíces de la ecuación $8x^2-3x=0\;$ .

Ejercicio 5 (3'34") Sinopsis:

Halla el discriminante para determinar el número de raíces de la ecuación $x^2+9=0\;$ .

Ejercicio 6 (6'58") Sinopsis:

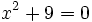Determinar el número de soluciones de la ecuación 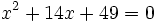$x^2+14x+49=0\;$ .

Discriminate y número de soluciones

Actividad 1 Descripción:

Actividades en la que aprenderás a calcular el discriminante de una ecuación de segundo grado y su utilidad para determinar el número de soluciones de la misma.

Actividad 2 Descripción:

Calcula el número de soluciones de una ecuación de segundo grado:

Pulsa el botón "Ejercicio" para obtener una ecuación.
Copia la ecuación en tu cuaderno y calcula su discriminante.
Teniendo en cuenta el valor del discriminante, determina cuántas soluciones tiene.
Escribe el número de soluciones en el cuadro "Número de soluciones" y pulsa el botón "Solución".

Autoevaluación 1 Descripción:

Ejercicios de autoevaluación sobre las soluciones de las ecuaciones de segundo grado.

Autoevaluación 2 Descripción:

Ejercicios de autoevaluación sobre las soluciones de las ecuaciones de segundo grado.

Obtenido de "http://www.maralboran.org/wikipedia/index.php/Plantilla:Discriminante_de_la_ecuaci%C3%B3n_de_segundo_grado"

 {{p}}
 {{Videotutoriales|titulo=Discriminante y número de soluciones|enunciado=
+{{Video_enlace_pildoras
+|titulo1=Tutorial
+|duracion=5'42"
+|sinopsis=Número de soluciones de una ecuación de 2º grado. Discriminante.
+|url1=https://youtu.be/8aZNrJM0v8k?list=PLwCiNw1sXMSCRy5LXaPOVwNMHxxxvNk0Z
+}}
+----
 {{Video_enlace_virtual
 |titulo1=Ejercicio 1

Plantilla:Discriminante de la ecuación de segundo grado

De Wikipedia

Revisión actual

Vistas

Herramientas personales

Menú

Buscar

Herramientas