Plantilla:Definición: ecuación de segundo grado

(Diferencia entre revisiones)

Revisión actual

Una ecuación de segundo grado con una incógnita, 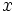$x\;\!$ , es aquella que tiene o se puede reducir a la siguiente expresión, que llamaremos forma general.

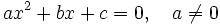
$ax^2+bx+c=0, \quad a\ne 0$

Si algún coeficiente,"b" o "c", es cero la ecuación diremos que es incompleta. En caso contrario diremos que es completa.

Ejemplos

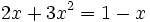$2x+3x^2=1-x\;$ es una ecuación de segundo grado completa, ya que se puede reducir a la siguiente forma general: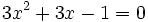 $3x^2+3x-1=0\;$
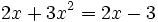$2x+3x^2=2x-3\;$ es una ecuación de segundo grado incompleta, ya que se puede reducir a la siguiente forma general: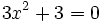 $3x^2+3=0\;$
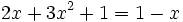$2x+3x^2+1=1-x\;$ es una ecuación de segundo grado completa, ya que se puede reducir a la siguiente forma general: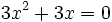 $3x^2+3x=0\;$
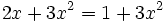$2x+3x^2=1+3x^2\;$ no es una ecuación de segundo grado, ya que al reducirla resulta una ecuación de primer grado: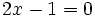 $2x-1=0\;$

La ecuación de segundo grado (3´38") Sinopsis:

Definición de ecuación de segundo grado.

La ecuación de segundo grado Descripción:

Actividades en la que aprenderás a identificar los coeficientes de una ecuación de segundo grado y a determinar si es completa o incompleta.

 }}
 {{p}}
+{{Video_enlace_pildoras
+|titulo1=La ecuación de segundo grado
+|duracion=3´38"
+|url1=https://youtu.be/Vg_3UTfJQn4?list=PLwCiNw1sXMSCRy5LXaPOVwNMHxxxvNk0Z
+|sinopsis=Definición de ecuación de segundo grado.
+}}
 {{AI_cidead
-|titulo1=Ecuaciones de segundo grado
+|titulo1=La ecuación de segundo grado
 |descripcion=Actividades en la que aprenderás a identificar los coeficientes de una ecuación de segundo grado y a determinar si es completa o incompleta.
 |url1=http://recursostic.educacion.es/secundaria/edad/3esomatematicas/3quincena3/3quincena3_contenidos_3a.htm
 }}