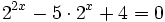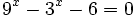Plantilla:Ecuaciones exponenciales
De Wikipedia
| Revisión de 10:53 6 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 97: | Línea 97: | ||
| }} | }} | ||
| - | {{p}} | ||
| - | {{wolfram desplegable|titulo=Ecuaciones exponenciales|contenido= | ||
| - | {{wolfram | ||
| - | |titulo=Actividad: ''Ecuaciones exponenciales'' | ||
| - | |cuerpo= | ||
| - | {{ejercicio_cuerpo | ||
| - | |enunciado= | ||
| - | |||
| - | Resuelve las siguientes ecuaciones: | ||
| - | |||
| - | :a) <math>3^x=\sqrt[3]{9} \;</math> | ||
| - | |||
| - | :b) <math>2^{2x}-5\cdot 2^x+4=0 \;</math> | ||
| - | |||
| - | :c) <math>9^x-3^x-6=0 \;</math> | ||
| - | {{p}} | ||
| - | |sol= | ||
| - | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| - | |||
| - | :a) {{consulta|texto=solve 3^x=3th root (9) over the reals}} | ||
| - | :b) {{consulta|texto=solve 2^(2x)-5*2^x+4=0 over the reals}} | ||
| - | :c) {{consulta|texto=solve 9^x-3^x-6=0 over the reals}} | ||
| - | |||
| - | {{widget generico}} | ||
| - | }} | ||
| - | }} | ||
| - | }} | ||
| - | {{p}} | ||
| - | |||
| {{p}} | {{p}} | ||
| {{Videotutoriales|titulo=Ecuaciones exponenciales | {{Videotutoriales|titulo=Ecuaciones exponenciales | ||
| |enunciado= | |enunciado= | ||
| {{Video_enlace_clasematicas | {{Video_enlace_clasematicas | ||
| - | |titulo1=Tutorial | + | |titulo1=Tutorial 1 |
| |duracion=22'26" | |duracion=22'26" | ||
| |sinopsis=Tutorial que trabaja las ecuaciones exponenciales, desde muy sencillas, en donde únicamente se utilizan las propiedades básicas de las potencias, hasta otras más completas en donde es necesario realizar un cambio de variable. | |sinopsis=Tutorial que trabaja las ecuaciones exponenciales, desde muy sencillas, en donde únicamente se utilizan las propiedades básicas de las potencias, hasta otras más completas en donde es necesario realizar un cambio de variable. | ||
| Línea 140: | Línea 111: | ||
| |url1=https://www.youtube.com/watch?v=htLzTGNZgfY&index=11&list=PLZNmE9BEzVInJZxxpaxecd3SH4TK5eggR | |url1=https://www.youtube.com/watch?v=htLzTGNZgfY&index=11&list=PLZNmE9BEzVInJZxxpaxecd3SH4TK5eggR | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 2a | ||
| + | |duracion=2'32" | ||
| + | |sinopsis=Ecuaciones exponenciales, que son aquellas con la x en el exponente. | ||
| + | |url1=https://youtu.be/lbD5r0_jbCA?list=PLwCiNw1sXMSAfvazFU32RCdaF4fbxqvl4 | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 2b | ||
| + | |duracion=5'32" | ||
| + | |sinopsis=Ejemplos de resolución de ecuaciones exponenciales. | ||
| + | |url1=https://www.youtube.com/watch?v=HV6rLZP_eAs&list=PLwCiNw1sXMSAfvazFU32RCdaF4fbxqvl4&index=2 | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 2c | ||
| + | |duracion=11'17" | ||
| + | |sinopsis=Más ejemplos de resolución de ecuaciones exponenciales. | ||
| + | |url1=https://www.youtube.com/watch?v=1NVBg4SUDbE&list=PLwCiNw1sXMSAfvazFU32RCdaF4fbxqvl4&index=3 | ||
| }} | }} | ||
| ---- | ---- | ||
| + | {{Tabla50|celda1= | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| |titulo1=Ejercicio 1 | |titulo1=Ejercicio 1 | ||
| Línea 150: | Línea 140: | ||
| :b) <math>7^{3-x}=5^{x+1}\;</math> | :b) <math>7^{3-x}=5^{x+1}\;</math> | ||
| - | |url1=https://www.youtube.com/watch?v=Fl1PvjOh9Us | + | |url1=http://www.youtube.com/watch?v=Fl1PvjOh9Us |
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| Línea 160: | Línea 150: | ||
| - | |url1=https://www.youtube.com/watch?v=_aZ10GXvUuM | + | |url1=http://www.youtube.com/watch?v=_aZ10GXvUuM |
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| Línea 170: | Línea 160: | ||
| - | |url1=https://www.youtube.com/watch?v=6ys1c3DIVNA | + | |url1=http://www.youtube.com/watch?v=6ys1c3DIVNA |
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| Línea 180: | Línea 170: | ||
| - | |url1=https://www.youtube.com/watch?v=nR3INhQWHGc | + | |url1=http://www.youtube.com/watch?v=nR3INhQWHGc |
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| Línea 200: | Línea 190: | ||
| - | |url1=https://www.youtube.com/watch?v=qA9Iggk09jQ | + | |url1=http://www.youtube.com/watch?v=qA9Iggk09jQ |
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| Línea 210: | Línea 200: | ||
| - | |url1=https://www.youtube.com/watch?v=iDKX--wp2U4 | + | |url1=http://www.youtube.com/watch?v=iDKX--wp2U4 |
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicio 8 | ||
| + | |duracion=10'35" | ||
| + | |sinopsis=Ejercicios de ecuaciones exponenciales. | ||
| + | |url1=http://www.youtube.com/watch?v=B3kcgResUhM&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=7 | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicio 9 | ||
| + | |duracion=8'39" | ||
| + | |sinopsis=Ejercicios de ecuaciones exponenciales. | ||
| + | |url1=http://www.youtube.com/watch?v=oPJyy-SsDws&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=8 | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicio 10 | ||
| + | |duracion=13'08" | ||
| + | |sinopsis=Ejercicios de ecuaciones exponenciales. | ||
| + | |url1=http://www.youtube.com/watch?v=pGAYYVEY0Y8&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=9 | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicio 11 | ||
| + | |duracion=6'52" | ||
| + | |sinopsis=Ejercicios de ecuaciones exponenciales. | ||
| + | |url1=http://www.youtube.com/watch?v=TXTCeoN1u24&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=11 | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Ejercicio 12 | ||
| + | |duracion=11'43" | ||
| + | |sinopsis=Ejercicios de ecuaciones exponenciales. | ||
| + | |url1=http://www.youtube.com/watch?v=lfS8f9B5xTg&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=12 | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 13 | ||
| + | |duracion=4´04" | ||
| + | |url1=http://www.youtube.com/watch?v=BMBpZaJCtWY&list=PLo7_lpX1yruMbDEv-X5EQe7uX0MEYspE-&index=1 | ||
| + | |sinopsis=Resuelve: <math>9^{log_3 \, x^{\frac{1}{2}}}=1 \;</math> | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 14 | ||
| + | |duracion=2´30" | ||
| + | |url1=http://www.youtube.com/watch?v=WidkUmsxeJY&list=PLo7_lpX1yruMbDEv-X5EQe7uX0MEYspE-&index=2 | ||
| + | |sinopsis=Resuelve: <math>2 \left(5^{log_5 \, x} \right)+3=3^{log_3 \, x}+2^{log_2 \, 5} \;</math> | ||
| + | }} | ||
| + | |celda2= | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 15 | ||
| + | |duracion=5´44" | ||
| + | |url1=http://www.youtube.com/watch?v=-qgRS8kLLxM&index=3&list=PLo7_lpX1yruMbDEv-X5EQe7uX0MEYspE- | ||
| + | |sinopsis=Resuelve: <math>4^{log_2 \, x}-3^{log_3 \, x}-7^{log_7 \, 2}=0 \;</math> | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 16 | ||
| + | |duracion=2´20" | ||
| + | |url1=http://www.youtube.com/watch?v=w6gWRbZrdYc&index=1&list=PLo7_lpX1yruNFL4jSLiWaBD7-V7pVOeB9 | ||
| + | |sinopsis=Resuelve: <math>5^{x-1}=25 \;</math> | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 17 | ||
| + | |duracion=4´02" | ||
| + | |url1=http://www.youtube.com/watch?v=QfdbV_6WqSA&list=PLo7_lpX1yruNFL4jSLiWaBD7-V7pVOeB9&index=2 | ||
| + | |sinopsis=Resuelve: <math>2^{x^2-2x}=8 \;</math> | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 18 | ||
| + | |duracion=3´10" | ||
| + | |url1=http://www.youtube.com/watch?v=esR9R9QHMIQ&list=PLo7_lpX1yruNFL4jSLiWaBD7-V7pVOeB9&index=3 | ||
| + | |sinopsis=Resuelve: <math>6^{2x+5}=36 \;</math> | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 19 | ||
| + | |duracion=4´38" | ||
| + | |url1=http://www.youtube.com/watch?v=JsJDEjfhl-4&list=PLo7_lpX1yruNFL4jSLiWaBD7-V7pVOeB9&index=4 | ||
| + | |sinopsis=Resuelve: <math>log_2 \, (9^{x-1}+7)=log_2 \, (3^{x-1}+1)^2 \;</math> | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 20 | ||
| + | |duracion=3´05" | ||
| + | |url1=http://www.youtube.com/watch?v=9-2W6nk1BEk&list=PLo7_lpX1yruNFL4jSLiWaBD7-V7pVOeB9&index=5 | ||
| + | |sinopsis=Resuelve: <math>49^{1-2x}=7^x\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 21 | ||
| + | |duracion=2´43" | ||
| + | |url1=http://www.youtube.com/watch?v=Z61bELdzJN0&index=6&list=PLo7_lpX1yruNFL4jSLiWaBD7-V7pVOeB9 | ||
| + | |sinopsis=Resuelve: <math>3^x=0.2\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 22 | ||
| + | |duracion=3´02" | ||
| + | |url1=http://www.youtube.com/watch?v=fnMamwb92mw&index=7&list=PLo7_lpX1yruNFL4jSLiWaBD7-V7pVOeB9 | ||
| + | |sinopsis=Resuelve: <math>(0.125)^x=128\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 23 | ||
| + | |duracion=4´50" | ||
| + | |url1=http://www.youtube.com/watch?v=qmh4YYUXrAo&index=8&list=PLo7_lpX1yruNFL4jSLiWaBD7-V7pVOeB9 | ||
| + | |sinopsis=Resuelve: <math>3^x=243^{x-2}\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 24 | ||
| + | |duracion=6´34" | ||
| + | |url1=http://www.youtube.com/watch?v=bjracVyQb2I&index=9&list=PLo7_lpX1yruNFL4jSLiWaBD7-V7pVOeB9 | ||
| + | |sinopsis=Resuelve: <math>25^x+5^{x+1}=750\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 25 | ||
| + | |duracion=6´52" | ||
| + | |url1=http://www.youtube.com/watch?v=BXTMKNHHbLk&index=10&list=PLo7_lpX1yruNFL4jSLiWaBD7-V7pVOeB9 | ||
| + | |sinopsis=Resuelve: <math>3^{-2x}+3^{-x}=2\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 26 | ||
| + | |duracion=6´31" | ||
| + | |url1=http://www.youtube.com/watch?v=GYowf71FzZ0&list=PLo7_lpX1yruNFL4jSLiWaBD7-V7pVOeB9&index=11 | ||
| + | |sinopsis=Resuelve: <math>e^x+2e^{-x}=3\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 27 | ||
| + | |duracion=10´55" | ||
| + | |url1=http://www.youtube.com/watch?v=cBE3xEYMUy4&index=12&list=PLo7_lpX1yruNFL4jSLiWaBD7-V7pVOeB9 | ||
| + | |sinopsis=Resuelve: <math>e^{2x}-2\sqrt{e^{2x+1}}=1-e\;</math> | ||
| + | }} | ||
| + | {{Video_enlace_virtual | ||
| + | |titulo1=Ejercicio 28 | ||
| + | |duracion=6´07" | ||
| + | |url1=http://www.youtube.com/watch?v=eJuXmkoxwgQ&index=13&list=PLo7_lpX1yruNFL4jSLiWaBD7-V7pVOeB9 | ||
| + | |sinopsis=Resuelve: <math>e^{2x}-e^{x+2}=e^{x+1}-e^3\;</math> | ||
| + | }} | ||
| + | }} | ||
| + | }} | ||
| + | {{Ejercicios_vitutor | ||
| + | |titulo1=Ejercicios: ''Ecuaciones exponenciales'' | ||
| + | |descripcion=Ejercicios resueltos sobre ecuaciones exponenciales. | ||
| + | |url1=http://www.vitutor.com/al/log/e_e.html | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{wolfram desplegable|titulo=Ecuaciones exponenciales|contenido= | ||
| + | {{wolfram | ||
| + | |titulo=Actividad: ''Ecuaciones exponenciales'' | ||
| + | |cuerpo= | ||
| + | {{ejercicio_cuerpo | ||
| + | |enunciado= | ||
| + | Resuelve las siguientes ecuaciones: | ||
| + | :a) <math>3^x=\sqrt[3]{9} \;</math> | ||
| + | |||
| + | :b) <math>2^{2x}-5\cdot 2^x+4=0 \;</math> | ||
| + | |||
| + | :c) <math>9^x-3^x-6=0 \;</math> | ||
| + | {{p}} | ||
| + | |sol= | ||
| + | Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: | ||
| + | |||
| + | :a) {{consulta|texto=solve 3^x=3th root (9) over the reals}} | ||
| + | :b) {{consulta|texto=solve 2^(2x)-5*2^x+4=0 over the reals}} | ||
| + | :c) {{consulta|texto=solve 9^x-3^x-6=0 over the reals}} | ||
| + | |||
| + | {{widget generico}} | ||
| + | }} | ||
| + | }} | ||
| }} | }} | ||
Revisión actual
Las ecuaciones exponenciales son aquellas en las que la incógnita aparece como exponente.
Para su resolución hay que tener en cuenta las propiedades de las potencias y también puede ser necesario usar logaritmos.
Ejercicios resueltos: Ecuaciones exponenciales
Resuelve las siguientes ecuaciónes:
- a)
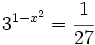
- b)
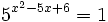
- c)
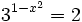
- d)
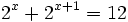
a)
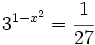
Expresamos el segundo miembro como potencia de 2:
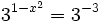
Como 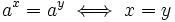 , los exponentes deben ser iguales:
, los exponentes deben ser iguales:
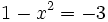
Y resolvemos la ecuación de segundo grado incompleta:
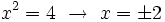
Soluciones: 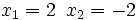
b)
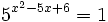
Expresamos el segundo miembro como potencia de 5:
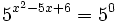
Como 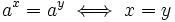 , los exponentes deben ser iguales:
, los exponentes deben ser iguales:
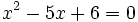
Resolvemos la ecuación de segundo grado:
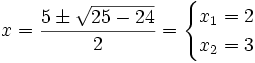
Soluciones: 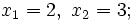
c)
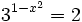
Como el segundo miembro no podemos expresarlo como potencia de base 3, tomaremos logaritmos en ambos lados de la ecuación:
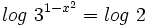
Aplicando la propiedad del logaritmo de una potencia:
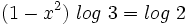
Y resolvemos la ecuación de segundo grado incompleta:
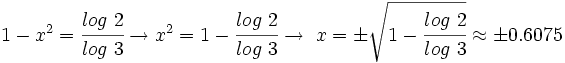
Soluciones: 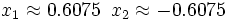
d)
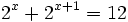
Haciendo el cambio de variable:
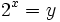
tenemos que:
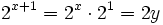
Y la ecuación de partida queda:

Resolvemos la ecuación de primer grado:
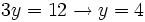
Y deshacemos el cambio de variable:
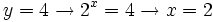
- Solución:
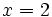
Tutorial que trabaja las ecuaciones exponenciales, desde muy sencillas, en donde únicamente se utilizan las propiedades básicas de las potencias, hasta otras más completas en donde es necesario realizar un cambio de variable.
- 00:00 a 01:15: Introducción y propiedad.
- 01:15 a 07:00: Ejercicios básicos, resolubles con las propiedades de las potencias.
- 07:00 a 11:55: Ejercicios de ecuaciones exponenciales usando el cambio de variable (primer grado).
- 11:55 a 22:26: Ejercicios de ecuaciones exponenciales usando el cambio de variable (segundo grado).
Ecuaciones exponenciales, que son aquellas con la x en el exponente.
Ejemplos de resolución de ecuaciones exponenciales.
Más ejemplos de resolución de ecuaciones exponenciales.
Resuelve:
Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Ejercicios de ecuaciones exponenciales. Ejercicios de ecuaciones exponenciales. Ejercicios de ecuaciones exponenciales. Ejercicios de ecuaciones exponenciales. Ejercicios de ecuaciones exponenciales. Resuelve: Resuelve: | Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: Resuelve: |
Ejercicios resueltos sobre ecuaciones exponenciales.
|
Actividad: Ecuaciones exponenciales Resuelve las siguientes ecuaciones:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
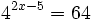
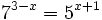
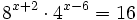
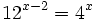
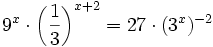
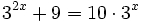
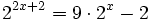
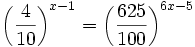
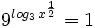
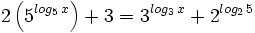
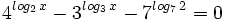
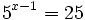
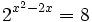
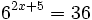
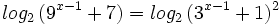
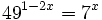
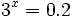
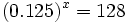
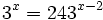
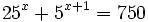
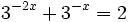
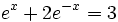
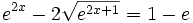
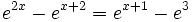
![3^x=\sqrt[3]{9} \;](/wikipedia/images/math/d/b/0/db0233292d84043ca9d4101f6ac692a6.png)