Plantilla:Razones trigonométricas de algunos ángulos importantes
De Wikipedia
| Revisión de 17:49 22 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| - | + | {{Tabla50|celda2=[[Imagen:rt_complementarios_triang.jpg|500px|center]] | |
| - | A continuación las razones trigonométricas de algunos ángulos que es conveniente recordar: | + | |celda1= |
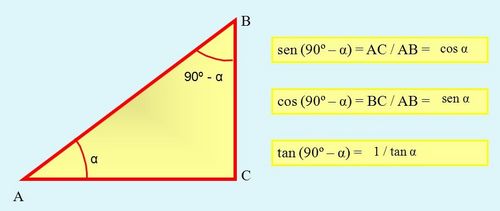
| + | {{Teorema_sin_demo|titulo=Razones trigonométricas de ángulos complementarios|enunciado= | ||
| + | Sea <math>\alpha \;</math> un ángulo y <math>90^\circ-\alpha \;</math> su complementario. | ||
| {{p}} | {{p}} | ||
| - | <center> | + | Se cumple que: |
| - | {| {{tablabonita_blanca}} | + | |
| - | |-style="background:#e1ecf7;" align="center" | + | |
| - | ! '''Grados''' | + | |
| - | ! sen | + | |
| - | ! cos | + | |
| - | ! tg | + | |
| - | ! cosec | + | |
| - | ! sec | + | |
| - | ! cot | + | |
| - | |----- | + | |
| - | | align="center" | <math>30^o \,</math> | + | |
| - | | align="center" | <math>\frac{1}{2}</math> | + | |
| - | | align="center" | <math>\frac{\sqrt{3}}{2}</math> | + | |
| - | | align="center" | <math>\frac{\sqrt{3}}{3}</math> | + | |
| - | | align="center" | <math>2 \,</math> | + | |
| - | | align="center" | <math>\frac{2\sqrt{3}}{3}</math> | + | |
| - | | align="center" | <math>\sqrt{3}</math> | + | |
| - | |----- | + | |
| - | | align="center" | <math>45^o \,</math> | + | |
| - | | align="center" | <math>\frac{\sqrt{2}}{2}</math> | + | |
| - | | align="center" | <math>\frac{\sqrt{2}}{2}</math> | + | |
| - | | align="center" | <math>1 \,</math> | + | |
| - | | align="center" | <math>\sqrt{2}</math> | + | |
| - | | align="center" | <math>\sqrt{2}</math> | + | |
| - | | align="center" | <math>1 \,</math> | + | |
| - | |----- | + | |
| - | | align="center" | <math>60^o \,</math> | + | |
| - | | <math>\frac{\sqrt{3}}{2}</math> | + | |
| - | | align="center" | <math>\frac{1}{2}</math> | + | |
| - | | align="center" | <math>\sqrt{3}</math> | + | |
| - | | align="center" | <math>\frac{2\sqrt{3}}{3}</math> | + | |
| - | | align="center" | <math>2 \,</math> | + | |
| - | | align="center" | <math>\frac{\sqrt{3}}{3}</math> | + | |
| - | |}</center> | + | |
| {{p}} | {{p}} | ||
| - | {{Geogebra_enlace | + | |
| - | |descripcion=En esta escena de Geogebra podrás ver como se calculan las razones trigonométricas de 30º, 45º y 60º con valores exactos. | + | :*<math>sen \, (90^\circ-\alpha)=cos \, \alpha</math> |
| - | |enlace=[https://ggbm.at/QXUgkgbK Razones trigonométricas de 30º, 45º y 60º] | + | |
| + | :*<math>cos \, (90^\circ-\alpha)= sen \, \alpha</math> | ||
| + | |||
| + | :*<math>tg \, (90^\circ-\alpha)=cot \, \alpha</math> | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Videotutoriales|titulo=Razones trigonométricas de ángulos complementarios|enunciado= | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=Tutorial 1 | ||
| + | |duracion=7´45" | ||
| + | |url1=https://youtu.be/3WRJpoQQc5M?list=PLwCiNw1sXMSCaukmrbPRm2SQuhas4kWS_ | ||
| + | |sinopsis=Relación entre el coseno, el seno y la tangente de ángulos complementarios. | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Tutorial 2 | ||
| + | |duracion=6´00" | ||
| + | |url1=https://www.youtube.com/watch?v=ue7XPdkptAw | ||
| + | |sinopsis=Relación entre el coseno y el seno de ángulos complementarios. | ||
| + | }} | ||
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| - | |titulo1=Razones trigonométricas de ángulos complementarios | + | |titulo1=Tutorial 3 |
| |duracion=4´54" | |duracion=4´54" | ||
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/05-angulos-agudos/04-razones-trigonometricas-de-angulos-complementarios#.VCfDrPl_u2E | + | |url1=https://www.youtube.com/watch?v=DREmTrfx3TQ&index=9&list=PLACC8661F6A8A59FA |
| - | |sinopsis=*Dos ángulos agudos se dicen complementarios si suman 90º. | + | |sinopsis=Razones trigonométricas de ángulos complementarios: |
| + | *Dos ángulos agudos se dicen complementarios si suman 90º. | ||
| *El seno de un ángulo agudo coincide con el coseno de su complementario. | *El seno de un ángulo agudo coincide con el coseno de su complementario. | ||
| *La tangente de un ángulo agudo coincide con la cotangente de su complementario. | *La tangente de un ángulo agudo coincide con la cotangente de su complementario. | ||
| - | *La secante de un ángulo agudo coincide con la cesecante de su complementario. | + | *La secante de un ángulo agudo coincide con la cosecante de su complementario. |
| - | + | }} | |
| + | ---- | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Ejercicio | ||
| + | |duracion=5´41" | ||
| + | |url1=https://www.youtube.com/watch?v=r_G1K1H52lQ | ||
| + | |sinopsis=Halla <math>sen\,32^\circ</math> sabiendo que <math>cos\,58^\circ \approx 0.53</math>. | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Problema | ||
| + | |duracion=6´17" | ||
| + | |url1=https://www.youtube.com/watch?v=AUS8sqvL7Q4 | ||
| + | |sinopsis=El rio Nilo se ha desbordado y ha inundado sus alrededores, a excepción de la punta de la pirámide de Guiza. Se ha enviado una expedición para averiguar la altura que alcanzó el agua. Los exploradores midieron el borde inclinado de la pirámide que quedó fuera del agua resultando ser de 72 m. Ellos saben además que la longitud total del borde es de 180 m y que la altura de la pirámide es de 139 m. ¿Cuál es la altura del agua sobre el nivel del suelo, redondeada a dos decimales? | ||
| + | }} | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Actividades | ||
| + | |descripcion=Razones trigonométricas de ángulos complementarios. | ||
| + | |url1=http://es.khanacademy.org/math/trigonometry/trigonometry-right-triangles/sine-and-cosine-of-complementary-angles/a/sine-and-cosine-are-cofunctions | ||
| }} | }} | ||
| - | {{p}} | ||
| - | {{Video_enlace_fonemato | ||
| - | |titulo1=Razones trigonométricas de los ángulos más famosos (0º, 30º, 45º, 60º, 90º) | ||
| - | |duracion=6´59" | ||
| - | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/05-angulos-agudos/05-razones-trigonometricas-de-los-angulos-mas-famosos#.VCfETfl_u2E | ||
| - | |sinopsis=*Apoyándonos en un triángulo equilátero de lado unidad, en este vídeo determinamos las razones trigonométricas de los ángulos de 30º y 60º. | ||
| - | *También determinamos las razones trigonométricas del ángulo de 45º; para ello nos servimos de un triángulo rectángulo de catetos unitarios. | ||
| - | *Las razones trigonométricas en cuestión deben memorizarse. | ||
| - | |||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Video_enlace_julioprofe | ||
| - | |titulo1=Razones trigonométricas de 0º, 30º, 45º, 60º y 90º (regla mnemotécnica) | ||
| - | |duracion=3´50" | ||
| - | |url1=https://www.youtube.com/watch?v=t5m2HBVF_uw | ||
| - | |sinopsis=Una regla mnemotécnica para obtener las razones trigonométricas de 0º, 30º, 45º, 60º y 90º }} | ||
Revisión actual
Razones trigonométricas de ángulos complementarios Sea Se cumple que: Relación entre el coseno, el seno y la tangente de ángulos complementarios. Relación entre el coseno y el seno de ángulos complementarios. Razones trigonométricas de ángulos complementarios:
Halla El rio Nilo se ha desbordado y ha inundado sus alrededores, a excepción de la punta de la pirámide de Guiza. Se ha enviado una expedición para averiguar la altura que alcanzó el agua. Los exploradores midieron el borde inclinado de la pirámide que quedó fuera del agua resultando ser de 72 m. Ellos saben además que la longitud total del borde es de 180 m y que la altura de la pirámide es de 139 m. ¿Cuál es la altura del agua sobre el nivel del suelo, redondeada a dos decimales? Razones trigonométricas de ángulos complementarios. |
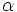 un ángulo y
un ángulo y 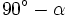 su complementario.
su complementario.
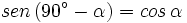
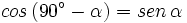
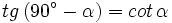
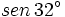 sabiendo que
sabiendo que 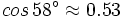 .
.