Plantilla:Videos: Regla de LHopital
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:28 29 mar 2020 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 2: | Línea 2: | ||
| |titulo=Regla de L'Hôpital | |titulo=Regla de L'Hôpital | ||
| |enunciado= | |enunciado= | ||
| - | {{Video_enlace | + | {{Video_enlace_matesandres |
| |titulo1=Tutorial 1 | |titulo1=Tutorial 1 | ||
| - | |duracion=17'28" | + | |duracion=11'41" |
| - | |sinopsis=Regla de l'Hopital. Ejemplos. | + | |sinopsis=Regla de l'Hopital para los casos de indeterminación básicos. Ejemplos. |
| - | |url1=https://youtu.be/whze02fAyco | + | |url1=https://youtu.be/TqXcx4rcvz8 |
| }} | }} | ||
| - | {{Video_enlace_fonemato | + | {{Video_enlace_unprofesor |
| |titulo1=Tutorial 2 | |titulo1=Tutorial 2 | ||
| - | |duracion=7'17" | + | |duracion=17'28" |
| - | |sinopsis=Video tutorial de matematicasbachiller.com | + | |sinopsis=Regla de l'Hopital para todos los casos de indeterminación. Ejemplos. |
| - | |url1=https://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/04-derivabilidad-de-funciones-2/27-regla-de-lhospital-2 | + | |url1=https://youtu.be/whze02fAyco |
| }} | }} | ||
| ---- | ---- | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejercicio 1 | + | |titulo1=Ejercicio 1a |
| |duracion=3'14" | |duracion=3'14" | ||
| |sinopsis=Calcula: <math>\lim_{x \to 1} \cfrac{1-x^2}{sen\,(\pi x)}</math> | |sinopsis=Calcula: <math>\lim_{x \to 1} \cfrac{1-x^2}{sen\,(\pi x)}</math> | ||
| Línea 23: | Línea 23: | ||
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejercicio 2 | + | |titulo1=Ejercicio 1b |
| |duracion=5'22" | |duracion=5'22" | ||
| |sinopsis=Calcula: <math>\lim_{n \to +\infty} \left( n \cdot sen\, \cfrac{\pi}{n} \right)</math> | |sinopsis=Calcula: <math>\lim_{n \to +\infty} \left( n \cdot sen\, \cfrac{\pi}{n} \right)</math> | ||
| Línea 30: | Línea 30: | ||
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| - | |titulo1=Ejercicio 3 | + | |titulo1=Ejercicio 1c |
| |duracion=3'26" | |duracion=3'26" | ||
| |sinopsis=Calcula: <math>\lim_{x \to 0} \cfrac{ln(1+6x)}{x}</math> | |sinopsis=Calcula: <math>\lim_{x \to 0} \cfrac{ln(1+6x)}{x}</math> | ||
| |url1=https://www.youtube.com/watch?v=4LlKgqB2SGk | |url1=https://www.youtube.com/watch?v=4LlKgqB2SGk | ||
| + | }} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejercicio 1d | ||
| + | |duracion=2'35" | ||
| + | |sinopsis=Calcula: <math>\lim_{x \to +\infty} \cfrac{6x^2+4x}{e^x+2}</math> | ||
| + | |||
| + | |url1=https://youtu.be/e2sH-m5DEb4 | ||
| }} | }} | ||
| {{Video_enlace_math2me | {{Video_enlace_math2me | ||
| - | |titulo1=Ejercicio 4 | + | |titulo1=Ejercicio 2a |
| |duracion=8'14" | |duracion=8'14" | ||
| |sinopsis=Calcula: <math>\lim_{x \to 3} \cfrac{\sqrt{x^2-5}}{x-3}</math> | |sinopsis=Calcula: <math>\lim_{x \to 3} \cfrac{\sqrt{x^2-5}}{x-3}</math> | ||
| Línea 44: | Línea 51: | ||
| }} | }} | ||
| {{Video_enlace_math2me | {{Video_enlace_math2me | ||
| - | |titulo1=Ejercicio 5 | + | |titulo1=Ejercicio 2b |
| |duracion=12'07" | |duracion=12'07" | ||
| - | |sinopsis=Calcula: <math>\lim_{x \to 0} \cfrac{x-sen \, x}}{2x^3}</math> | + | |sinopsis=Calcula: <math>\lim_{x \to 0} \cfrac{x-sen \, x}{2x^3}</math> |
| |url1=https://youtu.be/LMto5bx_bcU | |url1=https://youtu.be/LMto5bx_bcU | ||
| }} | }} | ||
| + | {{Video_enlace_math2me | ||
| + | |titulo1=Ejercicio 2c | ||
| + | |duracion=9'53" | ||
| + | |sinopsis=Calcula: <math>\lim_{x \to -1} \cfrac{x^2+2x+1}{x^4-1}</math> | ||
| + | |url1=https://youtu.be/qHcMrimIm4I | ||
| + | }} | ||
| + | {{Video_enlace_matesandres | ||
| + | |titulo1=Ejercicio 3 | ||
| + | |duracion=11'07" | ||
| + | |sinopsis=Regla de l'Hopital. Ejemplos en los que hay que aplicarla varias veces. | ||
| + | |url1=https://youtu.be/C8oXjhCsKGw | ||
| + | }} | ||
| }} | }} | ||
Revisión actual
Regla de l'Hopital para los casos de indeterminación básicos. Ejemplos.
Regla de l'Hopital para todos los casos de indeterminación. Ejemplos.
Calcula: 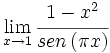
Calcula: 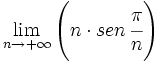
Calcula: 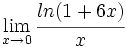
Calcula: 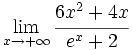
Calcula: 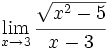
Calcula: 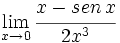
Calcula: 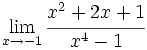
Regla de l'Hopital. Ejemplos en los que hay que aplicarla varias veces.

