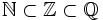Plantilla:El conjunto de los números racionales
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 07:42 30 ago 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 2: | Línea 2: | ||
| {{def cto racionales}} | {{def cto racionales}} | ||
| {{p}} | {{p}} | ||
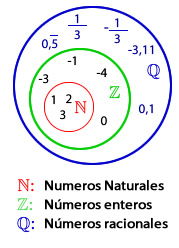
| - | Si el numerador es divisible por el denominador, la fracción representa a un número entero. Así, los racionales contienen a los enteros y éstos a los naturales. | + | {{Teorema_sin_demo|titulo=Obseva que:|enunciado= |
| - | + | *Si el numerador es divisible por el denominador, la fracción representa a un número entero. Así, los racionales contienen a los enteros y éstos a los naturales. | |
| + | {{p}} | ||
| {{Caja|contenido= | {{Caja|contenido= | ||
| <center><math>\mathbb{N}\sub\mathbb{Z}\sub\mathbb{Q}</math></center> | <center><math>\mathbb{N}\sub\mathbb{Z}\sub\mathbb{Q}</math></center> | ||
| + | }} | ||
| + | *Todos los números decimales exactos o periódicos se pueden expresar en forma de fracción. Por tanto, son números racionales. | ||
| + | *Cuando el número de decimales es infinito y no periódico, como ocurre con el número pi <math>(\pi)</math>, no podemos expresarlo en forma de fracción. A estos números los llamaremos '''[[Números irracionales|irracionales]]'''. | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Teorema|titulo=Proposición|enunciado=La suma y el producto de dos números racionales es otro número racional. | ||
| + | |demo= | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Demostración: ''La suma y el producto de dos racionales es racional'' | ||
| + | |duracion=4´05" | ||
| + | |sinopsis=Demostración de que la suma y el producto de dos racionales es racional. | ||
| + | |url1=https://youtu.be/rDCvtV4QVAg | ||
| + | }} | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_profealex | ||
| + | |titulo1=El conjunto de los números racionales | ||
| + | |duracion=7'42" | ||
| + | |sinopsis=El conjunto de los números racionales | ||
| + | |url1=https://youtu.be/kYyDc0XRUeg?list=PLeySRPnY35dFK2lF2mu30NYq-79SYEwuz | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=El conjunto de los números racionales | ||
| + | |duracion=4'38" | ||
| + | |sinopsis=El conjunto de los números racionales | ||
| + | |url1=https://youtu.be/c9eWZ5zlzP0 | ||
| + | }} | ||
| + | {{Video_enlace | ||
| + | |titulo1=Números racionales e irracionales | ||
| + | |duracion=3'08" | ||
| + | |sinopsis=El conjunto de los números racionales. | ||
| + | |url1=https://youtu.be/vj26kX-9Zi4 | ||
| + | }} | ||
| + | {{Video_enlace_khan | ||
| + | |titulo1=Números racionales e irracionales | ||
| + | |duracion=8'58" | ||
| + | |sinopsis=Introducción a números racionales e irracionales. | ||
| + | |url1=https://www.youtube.com/watch?v=-rP_MAluiKA | ||
| }} | }} | ||
| }} | }} | ||
Revisión actual
El conjunto de los números racionales es el conjunto de todas las fracciones: 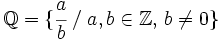  Obseva que:
Proposición La suma y el producto de dos números racionales es otro número racional. Demostración:  Demostración: La suma y el producto de dos racionales es racional (4´05") Sinopsis: Demostración de que la suma y el producto de dos racionales es racional.  El conjunto de los números racionales (7'42") Sinopsis: El conjunto de los números racionales  El conjunto de los números racionales (4'38") Sinopsis:El conjunto de los números racionales  Números racionales e irracionales (3'08") Sinopsis:El conjunto de los números racionales. Números racionales e irracionales (8'58") Sinopsis: Introducción a números racionales e irracionales. |  |
