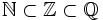Plantilla:El conjunto de los números racionales
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 09:20 26 ene 2018 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 12: | Línea 12: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{Teorema|titulo=Proposición|enunciado=La suma y el producto de dos números racionales es otro racional. | + | {{Teorema|titulo=Proposición|enunciado=La suma y el producto de dos números racionales es otro número racional. |
| |demo= | |demo= | ||
| - | {{Video_enlace | + | {{Video_enlace_khan |
| |titulo1=Demostración: ''La suma y el producto de dos racionales es racional'' | |titulo1=Demostración: ''La suma y el producto de dos racionales es racional'' | ||
| |duracion=4´05" | |duracion=4´05" | ||
| Línea 22: | Línea 22: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Video_enlace_profealex | ||
| + | |titulo1=El conjunto de los números racionales | ||
| + | |duracion=7'42" | ||
| + | |sinopsis=El conjunto de los números racionales | ||
| + | |url1=https://youtu.be/kYyDc0XRUeg?list=PLeySRPnY35dFK2lF2mu30NYq-79SYEwuz | ||
| + | }} | ||
| + | {{Video_enlace_pildoras | ||
| + | |titulo1=El conjunto de los números racionales | ||
| + | |duracion=4'38" | ||
| + | |sinopsis=El conjunto de los números racionales | ||
| + | |url1=https://youtu.be/c9eWZ5zlzP0 | ||
| + | }} | ||
| + | {{Video_enlace | ||
| + | |titulo1=Números racionales e irracionales | ||
| + | |duracion=3'08" | ||
| + | |sinopsis=El conjunto de los números racionales. | ||
| + | |url1=https://youtu.be/vj26kX-9Zi4 | ||
| + | }} | ||
| {{Video_enlace_khan | {{Video_enlace_khan | ||
| |titulo1=Números racionales e irracionales | |titulo1=Números racionales e irracionales | ||
Revisión actual
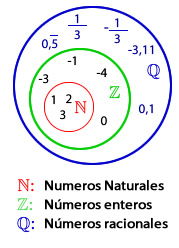
El conjunto de los números racionales es el conjunto de todas las fracciones: 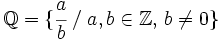 Obseva que:
Proposición La suma y el producto de dos números racionales es otro número racional. Demostración: Demostración de que la suma y el producto de dos racionales es racional. El conjunto de los números racionales El conjunto de los números racionales El conjunto de los números racionales. Introducción a números racionales e irracionales. |